理解对极几何与基本矩阵
对极几何是双视图之间内在的射影几何。它独立于景物结构,只依赖于摄像机的内参外参。
而基本矩阵是对对极几何的代数表示。
对极几何
如下图所示,对极几何通常用来解决双眼匹配搜索对应点的问题。
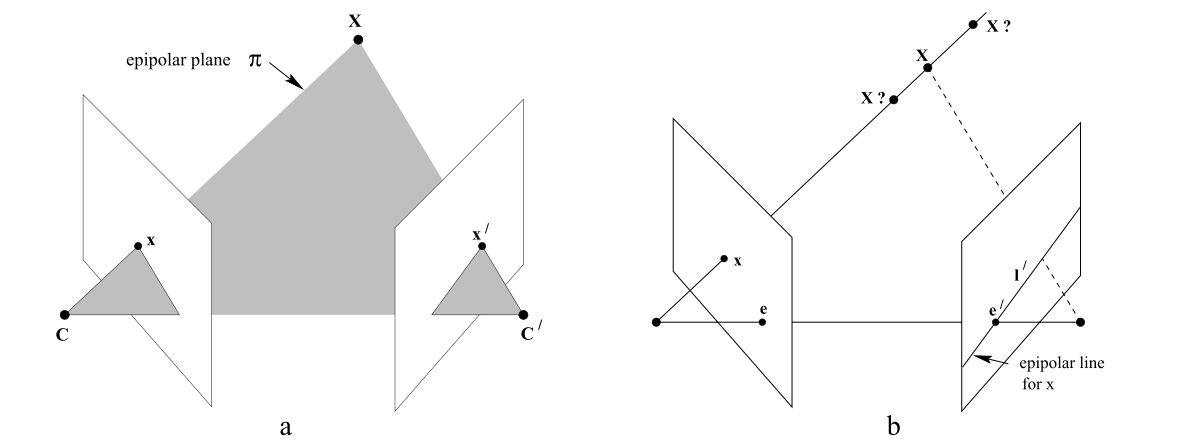
上图a中两个摄像机的中心分别是C与C',而X为一个三维空间点,它在两个摄像机的成像平面上的投影点分别是x与x'。我们常称: - 基线:两个摄像机光心的连线\(CC'\) - 对极点:上图b中的e与e',它们分别是一幅视图中另一个摄像机中心的像。二维表示为基线\(CC'\)与两个成像平面的交点。 - 对极平面:是一张包含基线的平面,存在着对极平面的一个集合(以基线为轴转动),上图中的一个例子就是\(CXC'\)。 - 对极线:对极平面与图像平面的交线。上图中的例子是\(xe\)与\(x'e'\),一个成像平面上的所有的对极线相交于对极点。
上图中还体现了一些性质,对于一幅图像上的每一点x,在第二幅图像上,任何与该点x匹配的点x'必然在对极线I'上,该对极线是过点x与第一个摄像机中心C的射线在第二幅图像上的投影。
基本矩阵F
由上面的讲述,我们知道,在深度未知的情况下,对于一幅图像上的一点x,映射在另一幅图像上是一条与之对应的对极线I'。
\[ x \rightarrowtail I' \]
基本矩阵F表示的正是这个从一个点到一条直线的射影映射。
由上,我们发现基本矩阵F实现的是从二维(二维点)到一维(一条线上的点)的转换,因此F的秩只能是2。
推导出基础矩阵与本质矩阵
由相机成像的几何描述我们可以理解如下的公式(世界坐标到像素坐标的转换):
\[ Z_1p_{uv1} = K_1P_w \]
\[ Z_2p_{uv2} = K_2(RP_w + t) \]
其中K是相机内参,R与t是第二个相机在第一个相机的相机坐标系下的外参,\(P_w\)是此空间点在第一个相机的相机坐标系下的坐标。Z是空间点到相机光心的距离(也是相机坐标系下的z轴坐标)。\(p_{uv1}\)与\(p_{uv2}\)是空间点\(P_w\)在两个相机平面上的投影点。
- 首先做出如下定义(其中\(x_1\)与\(x_2\)是归一化的相机坐标(X/Z,Y/Z,1)):
\[ x_1 = K_1^{-1}p_{uv1} \]
\[ x_2 = K_2^{-1}p_{uv2} \]
- 带入如上定义可得:
\[ Z_2 x_2 = Z_1 Rx_1 + t \]
- 上式两边同时左乘
t^,也就是两侧同时与t做外积:
\[ Z_2 t^{\land} x_2 = Z_1 t^{\land} R x_1 \]
- 两侧同时左乘\(x_{2}^T\):
\[ Z_2 x_{2}^T t^{\land} x_2 = Z_1 x_{2}^T t^{\land} R x_1 \]
- 上式中由于等式左侧 \(t^{\land} x_2\) 是一个与t、\(x_2\)都垂直的向量,再和\(x_2\)做内积将得到0,因此上式子其实可以写成如下形式:
\[ x_{2}^T t^{\land} R x_1 = 0 \]
- 上式就是大名鼎鼎的対极约束,将 \(x_1\) 与 \(x_2\) 换下,重新带入 \(p_{uv1}\) 与 \(p_{uv2}\) 可得:
\[ p_{uv2}^T K_2^{-T} t^{\land} R K_1^{-1} p_{uv1} = 0 \]
- 其中,中间项就是基础矩阵,满足如下:
\[ p_{uv2}^T F p_{uv1} = 0 \]
\[ F = K_2^{-T} t^{\land} R K_1^{-1} \]
此处注意,当点\(p_{uv1}\)与基础矩阵F确定时,上式演变成一个直线方程,更好的诠释了基础矩阵的本质是从一个点到一条直线的射影映射的代数表示。
- 本质矩阵是基础矩阵中只与外参相关的部分,即去掉相机内参,可以得到:
\[ E = t^{\land} R \]
\[ F = K_2^{-T} E K_1^{-1} \]
基础矩阵与本质矩阵的性质
本质矩阵是两个矩阵的乘积,其中R的秩为3(满秩),\(t^{\land}\)的秩为2,因此E的秩为2。
基础矩阵是四个矩阵的乘积,其中只有\(t^{\land}\)的秩为2,其他的三个都是满秩的(为3),最终秩也为2。
基础矩阵是四个矩阵的乘积,其中左右相机内参矩阵待定参数各4个,平移自由度是3,旋转自由度也是3,因此总共应该是14个待定参数。但是实际上F是一个\(3 \times 3\)的矩阵,总共9个参数,所以它最大自由度是9。又因为F满足以下两个约束,所以F的自由度其实是\(9-2=7\)。
- 尺度等价性
- def(f)=0
本质矩阵的自由度由平移与旋转的各三个自由度组成,加上尺度等价性,因此本质矩阵自由度为5。
对极约束条件的探讨
一般在slam中,可以通过本质矩阵E的奇异值分解得到相机相对于前一时刻的位姿变换。
但是在只有旋转没有平移时,対极约束是恒成立的,此时不能用本质矩阵进行相机的位姿估计。
対极约束条件是尺度无关的,所以恢复出来的的位姿变换具有尺度的不确定性。
基础矩阵与本质矩阵的求解
由上面我们知道基础矩阵自由度为7,所以最少我们可以使用7对点来求解基础矩阵。同样,本质矩阵自由度是5,我们最小可以使用5对点进行求解。但是因为它们的内在性质中很多都是非线性的性质,因此使用最少的点数求解会比较麻烦,所以一般情况下,只考虑尺度等价性,然后使用8对点进行求解。这也叫作八点法。
考虑一对匹配点,它们的像素坐标(如果是求解本质矩阵,那就是归一化坐标)为\(x_1 = [u_1, v_1, 1]^T, x_2 = [u_2, v_2, 1]^T\)。根据对极约束,有:
\[ \left(u_{2}, v_{2}, 1\right)\left(\begin{array}{lll}{e_{1}} & {e_{2}} & {e_{3}} \\ {e_{4}} & {e_{5}} & {e_{6}} \\ {e_{7}} & {e_{8}} & {e_{9}}\end{array}\right)\left(\begin{array}{l}{u_{1}} \\ {v_{1}} \\ {1}\end{array}\right)=0 \]
将上面矩阵展开,写成向量的形式(为了后续好解):
\[ e=\left[e_{1}, e_{2}, e_{3}, e_{4}, e_{5}, e_{6}, e_{7}, e_{8}, e_{9}\right]^{\mathrm{T}} \]
此时上面对极约束的等式可以写成如下的形式
\[ \left[u_{2} u_{1}, u_{2} v_{1}, u_{2}, v_{2} u_{1}, v_{2} v_{1}, v_{2}, u_{1}, v_{1}, 1\right] \cdot e=0 \]
将八个点的对极约束放在一起便可以得到一个方程组:
\[ \left(\begin{array}{cccccccc}{u_{2}^{1} u_{1}^{1}} & {u_{2}^{1} v_{1}^{1}} & {u_{2}^{1}} & {v_{2}^{1} u_{1}^{1}} & {v_{2}^{1} v_{1}^{1}} & {v_{2}^{1}} & {u_{1}^{1}} & {v_{1}^{1}} & {1} \\ {u_{2}^{2} u_{1}^{2}} & {u_{2}^{2} v_{1}^{2}} & {u_{2}^{2}} & {v_{2}^{2} u_{1}^{2}} & {v_{2}^{2} v_{1}^{2}} & {v_{2}^{2}} & {u_{1}^{2}} & {v_{1}^{2}} & {1} \\ {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} \\ {u_{2}^{8} u_{1}^{8}} & {u_{2}^{8} v_{1}^{8}} & {u_{2}^{8}} & {v_{2}^{8} u_{1}^{8}} & {v_{2}^{8} v_{1}^{8}} & {v_{2}^{8}} & {u_{1}^{8}} & {v_{1}^{8}} & {1}\end{array}\right)\left(\begin{array}{c}{e_{1}} \\ {e_{2}} \\ {e_{3}} \\ {e_{4}} \\ {e_{5}} \\ {e_{6}} \\ {e_{7}} \\ {e_{8}} \\ {e_{9}}\end{array}\right) = 0 \]
解方程组便可以求解出本质矩阵或基础矩阵。
通过本质矩阵恢复处R与T
在上述工作完成求解出本质矩阵E之后,可以通过SVD分解得到如下等式
\[ \boldsymbol{E}=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\mathrm{T}} \]
其中U和V是正交阵,中间\(\boldsymbol{\Sigma}\)是奇异值矩阵。根据E的内在性质,我们知道\[\boldsymbol{\Sigma} = diag(\mu, \mu, 0)\]。通过SVD分解,任意一个E,存在两个可能的R和t与其对应。
\[ \begin{array}{l}{t_{1}^{\wedge}=U R_{Z}\left(\frac{\pi}{2}\right) \Sigma U^{\mathrm{T}}, \quad R_{1}=U R_{Z}^{\mathrm{T}}\left(\frac{\pi}{2}\right) V^{\mathrm{T}}} \\ {t_{2}^{\wedge}=U R_{Z}\left(-\frac{\pi}{2}\right) \Sigma U^{\mathrm{T}}, \quad R_{2}=U R_{Z}^{\mathrm{T}}\left(-\frac{\pi}{2}\right) V^{\mathrm{T}}}\end{array} \]
其中\[R_{Z}\left(\frac{\pi}{2}\right)\]表示沿Z轴旋转90°得到的旋转矩阵。同时由于E无论是否取符号都是等价的,因此对上面得到的t取负号也会得到相同的结果。因此每个E通过分解一共有四种可能的解。
参考资料
- [1] 《Multiple View Geometry in Computer Vision (Second Edition)》
- [2] 《视觉slam十四讲》