关于旋转或姿态的扰动求导问题总结
下面1,2两节都是在哈密顿形式的姿态上进行讨论的,第三节开始涉及JPL与哈密顿的区别。
1 对于可加法因变量的扰动求导
因为加法本身是无向的(左右等价),所以没有左右扰动的概念。但是对于旋转矩阵群,左乘和右乘是不等价的,因此左右扰动的概念仅仅在不适用加法的群上存在。
1.1 左扰动雅克比
\[ \begin{aligned} \frac{\partial(\boldsymbol{R} \boldsymbol{p})}{\partial \boldsymbol{\varphi}} &=\lim _{\varphi \rightarrow 0} \frac{\exp \left(\boldsymbol{\varphi}^{\wedge}\right) \boldsymbol{R} \boldsymbol{p}- \boldsymbol{R} \boldsymbol{p}}{\varphi} \\ &=\lim _{\varphi \rightarrow 0} \frac{\left(\boldsymbol{I}+\boldsymbol{\varphi}^{\wedge}\right) \boldsymbol{R} \boldsymbol{p} - \boldsymbol{R} \boldsymbol{p}}{\varphi} \\ &=\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{\boldsymbol{\varphi}^{\wedge} \boldsymbol{R} \boldsymbol{p}}{\varphi} =\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{-(\boldsymbol{R} \boldsymbol{p})^{\wedge} \boldsymbol{\varphi}}{\varphi} =-(\boldsymbol{R} \boldsymbol{p})^{\wedge} \end{aligned} \]
1.2 右扰动雅克比
\[ \begin{aligned} \frac{\partial(\boldsymbol{R} \boldsymbol{p})}{\partial \boldsymbol{\varphi}} &=\lim _{\varphi \rightarrow 0} \frac{ \boldsymbol{R} \exp \left(\boldsymbol{\varphi}^{\wedge}\right) \boldsymbol{p}- \boldsymbol{R} \boldsymbol{p}}{\varphi} \\ &=\lim _{\varphi \rightarrow 0} \frac{ \boldsymbol{R} \left(\boldsymbol{I}+\boldsymbol{\varphi}^{\wedge}\right) \boldsymbol{p} - \boldsymbol{R} \boldsymbol{p}}{\varphi} \\ &=\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{\boldsymbol{R} \boldsymbol{\varphi}^{\wedge} \boldsymbol{p}}{\varphi} =\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{-\boldsymbol{R} {\boldsymbol{p}}^{\wedge} \boldsymbol{\varphi}}{\varphi} =-\boldsymbol{R} {\boldsymbol{p}}^{\wedge} \end{aligned} \]
上述两种扰动中都利用了\(a^{\wedge} b = - b^{\wedge} a\)的性质,这个性质几何上很好理解,即交换叉乘的顺序,得到的结果是相反方向的。
2. 对于不可加法因变量的扰动求导
旋转矩阵群上加法不成立,乘法具有各向异性,假设如下都是哈密顿形式的姿态存储,则单纯求导有如下四种情况。(JPL也是四种,仅仅扰动形式稍有不同,可以查看第三节)。实际应用中会简单很多,因为通常哈密顿仅仅会进行右扰动,JPL仅仅会进行左扰动(因为通常都是在局部坐标系上添加扰动)。
假设因变量为\(R = R_1R_2\),自变量为\(R_1\)和\(R_2\),此时,假设我们先求R对\(R_1\)的雅克比(对\(R_2\)的雅克比类似),则情况可以分为四种:
- R的右扰动对\(R_1\)的右扰动求导:
\[ \begin{aligned} (R_1R_2)Exp(\theta) &= R_1 Exp(\phi)R_2 \\ (R_1R_2)Exp(\theta) &= R_1 R_2 Exp(R_2^T \phi) \\ Exp(\theta) &= Exp(R_2^T \phi) \\ J &= R_2^T \end{aligned} \]
- R的右扰动对\(R_1\)的左扰动求导:
\[ \begin{aligned} (R_1R_2)Exp(\theta) &= Exp(\phi) R_1 R_2 \\ Exp(\theta) &= R_2^T R_1^T Exp(\phi) R_1 R_2 \\ Exp(\theta) &= R_2^T Exp( R_1^T \phi) R_2 \\ Exp(\theta) &= Exp( R_2^T R_1^T \phi) \\ J &= R_2^T R_1^T \end{aligned} \]
- R的左扰动对\(R_2\)的左扰动求导:
- R的左扰动对\(R_2\)的右扰动求导:
上述求导中大量使用了矩阵的伴随性质。
3 左扰动与右扰动
在导航中,我们一般会定义两个主要的坐标系,分别是全局(Global,比如enu)坐标系与局部(Local,常常为运动物体的body坐标系)坐标系,其中全局坐标系最好是固定的。物体的姿态其实是相对坐标系定义的,所以在添加的扰动可以理解为是对坐标系的扰动,因此需要添加扰动时最好是对局部坐标系进行扰动(我的理解是全局坐标系的扰动容易导致出现整体的偏移,影响结果),假设对局部坐标系的扰动为\(\mathbf{R}_{\tilde{L}}^{L} = exp \left({\theta}_{L'}^{L}\right)\)(含义是从L'到L的旋转变换)。
因此当姿态表达在全局坐标系时(哈密顿,从局部坐标系矢量到全局坐标系矢量的旋转变换,从下标到上标),根据旋转的叠加方式,需要添加的是右扰动,即: \[ \mathbf{R}_{\tilde{L}}^{G} = \mathbf{R}_{L}^{G} \mathbf{R}_{\tilde{L}}^{L} = \mathbf{R}_{L}^{G}(I + \lfloor{\theta}_{L'} ^{L} \rfloor) \] 当姿态表达在局部坐标系时(JPL,旋转矩阵为从全局坐标系到局部坐标系的旋转变换,从下标到上标),根据旋转的叠加方式,需要添加的是左扰动,即: \[ \mathbf{R}_{G}^{L'} = \mathbf{R}_{L}^{L'} \mathbf{R}_{G}^{L} = (I +\lfloor {\theta}_{L} ^{L'} \rfloor) \mathbf{R}_{G}^{L} = (I - \lfloor{\theta}_{L'} ^{L} \rfloor) \mathbf{R}_{G}^{L} \]
查看一个项目中是使用什么形式的扰动,只需要查看a.姿态的表示形式,b.其获得更新量后对姿态的更新方式即可。接下来是重点!
- 比如openvins中姿态表示使用JPL,更新方式是首先将扰动三维向量dx转为单位四元数\(dq=[\frac{1}{2}\bf{dx},1]\),然后使用dq左乘原本的姿态q,因为上述dq转换为矩阵为\(dR = I_{3\times3}-\lfloor \bf{dx} \rfloor\),因此openvins中计算雅克比时需要是左扰动并且是左乘$(I - _{L'} ^{L} ) $的扰动形式。
- 如果有一个项目中姿态表示使用哈密顿,更新方式是首先将扰动三维向量dx转为单位四元数\(dq=[\frac{1}{2}\bf{dx},1]\),然后使用dq右乘原本的姿态q,因为上述dq转换为矩阵为\(dR = I_{3\times3}+\lfloor \bf{dx} \rfloor\),因此此项目中计算雅克比时需要是右扰动并且是右乘$(I + _{L'} ^{L}) $的扰动形式。
总结:根据你想在局部坐标系上添加扰动还是在全局坐标系上确定是左扰动还是右扰动。根据是JPL还是哈密顿决定扰动的形式\(exp(\theta)\)或\(exp(-\theta)\))。注意!::上述的旋转矩阵的叠加全都是从右向左的叠加,这是因为在对一个向量进行旋转时通常都是右乘这个向量,因此旋转叠加是从右向左叠加。
经过上述叙述,我们可以总结:
- 对于JPL形式的四元数表示的旋转,其表示的的姿态转换成旋转矩阵为\(\mathbf{R}_{G}^{L}\),该旋转矩阵可以将一个全局坐标系下的向量变换到局部坐标系下,即\({}^L\mathbf{p} =\mathbf{R}_{G}^{L} {}^G \mathbf{p}\)。当body运动,局部坐标系变化为\(L'\)时,可以添加左扰动
\[ \mathbf{R}_{G}^{L'} = \mathbf{R}_{L}^{L'} \mathbf{R}_{G}^{L} \\ {}^{L'}\mathbf{p} =\mathbf{R}_{G}^{L'} {}^G \mathbf{p} = \mathbf{R}_{L}^{L'} \mathbf{R}_{G}^{L} {}^G \mathbf{p} \]
- 对于哈密顿形式的四元数表示的旋转,其表示的的姿态转换成旋转矩阵为\(\mathbf{R}_{L}^{G}\),该旋转矩阵可以将一个局部坐标系下的向量变换到全局坐标系下,即\({}^G\mathbf{p} =\mathbf{R}_{L}^{G} {}^L \mathbf{p}\)。当body运动,局部坐标系变化为\(L'\)时,可以添加右扰动
\[ \mathbf{R}_{L'}^{G} = \mathbf{R}_{L}^{G} \mathbf{R}_{L'}^{L} \\ {}^{G}\mathbf{p} =\mathbf{R}_{L'}^{G} {}^{L'} \mathbf{p} = \mathbf{R}_{L}^{G} \mathbf{R}_{L'}^{L} {}^{L'} \mathbf{p} \]
- 由上可知,JPL与哈密顿在局部坐标系添加的扰动分别为\(\mathbf{R}_{L}^{L'}\)与\(\mathbf{R}_{L'}^{L}\),这二者互为反变换。一般空间坐标系为右手系,一般旋转向量通过右手法则定义。假设局部载体以z轴为旋转轴,右手法则旋转角度为\(\theta\),则旋转向量为\(\mathbf{\Theta} = [0,0,\theta]^{\top}\),从\(L\)变换到\(L'\)。则此时有
\[ \mathbf{q}_{jpl} \approx [\frac{1}{2}\mathbf{\Theta}, 1] \\ C(\mathbf{q}_{jpl}) = \mathbf{R}_{L}^{L'} = exp(-\lfloor \mathbf{\Theta} \rfloor)\\ \mathbf{q}_{hamilton} \approx [\frac{1}{2}\mathbf{\Theta}, 1] \\ C(\mathbf{q}_{hamilton}) =\mathbf{R}_{L'}^{L} = exp(\lfloor \mathbf{\Theta} \rfloor) \]
其中\(C()\)表示将四元数变为对应的旋转矩阵,其中比较容易误解的一点是,载体从\(L\)到\(L'\)的旋转向量为\(\mathbf{\Theta}\),但是对应的\(\mathbf{R}_{L}^{L'} = exp(-\lfloor \mathbf{\Theta} \rfloor)\),这是因为该旋转矩阵表示的是将坐标系\(L\)中的向量变换到\(L'\)坐标系中,这和坐标系本身的变换是刚好相反的。也正因为这一点,才有\(\mathbf{R}_{L'}^{L} = exp(\lfloor \mathbf{\Theta} \rfloor)\)。
- 上述描述中涉及到了旋转向量,旋转向量可以表示为\(\theta\mathbf{r}\),其中\(\theta\)为旋转角度,\(\mathbf{r}\)为旋转轴,其表示的旋转通过右手定则定义。对于一个三维点\(\mathbf{p}\),其通过该旋转向量变换后得到的三维点为\(\mathbf{p'}\)为
\[ \mathbf{p'} = \cos\theta \cdot \mathbf{p} +(1-\cos\theta)(\mathbf{p\cdot r})\mathbf{r} + \sin\theta \cdot \mathbf{r} \times\mathbf{p} \]
可以发现,旋转向量的旋转轴方向上的向量在经过该旋转变换后不变,因此旋转向量的旋转轴既可以看做是定义在原坐标系中,也可以看做是定义在旋转后的坐标系中。
4. 旋转的叠加方式与系统中四元数表达方式的关系
上面讲了添加扰动需要遵从旋转的叠加方式。而旋转的叠加方式与系统中四元数的表达方式有关。
其实四元数的JPL格式(基于左手定则)与汉密尔顿格式(基于右手定则)的内容有不少,此处就不详细展开了。只指出几点如下,将四元数转成旋转矩阵,JPL与汉密尔顿得到的旋转矩阵是不同的,并且满足如下关系。
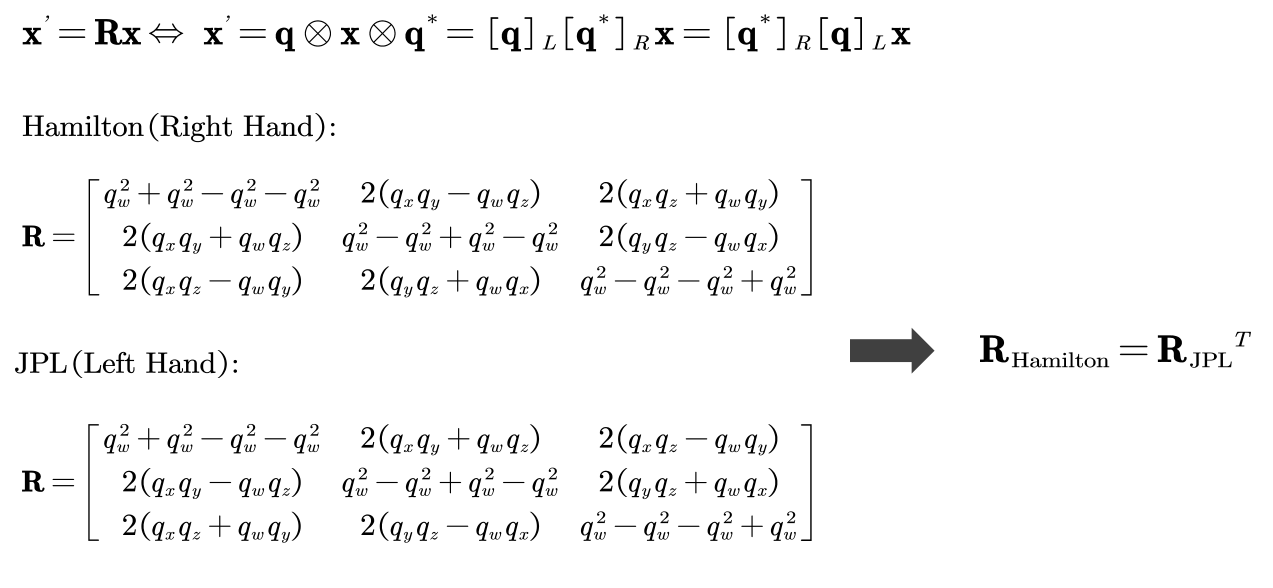
由于这个性质,所以对于一个旋转向量扰动\(\delta \theta\),其构造四元数为\([1,\frac{1}{2} \delta\theta]\)。对于这个四元数,哈密顿定则下其对应的旋转矩阵为\(I+[\delta \theta_{\times}]\),JPL定则下其对应的旋转矩阵为\(I-[\delta \theta_{\times}]\)
我们发现这两个旋转矩阵互为转置,因此在这两种四元数的表示方式下的系统姿态旋转矩阵的叠加方式是刚好相反的。可以参考,第3节,其中第一个式子就是汉密尔顿表示的位姿的旋转矩阵的叠加,一般添加右扰动;第二个式子是JPL表示的位姿的旋转矩阵的叠加。
黄国权老师的openvins就是使用了jpl的姿态表示形式。北航的很多滤波slam工作都是使用了哈密顿的姿态表示形式。根据上述分析可以发现,JPL还有哈密顿主要是决定了在系统中存储的姿态与坐标系之间相对变换的形式。哈密顿表示的姿态其实是全局坐标系到局部坐标系的旋转,JPL表示的姿态其实是从局部坐标系到全局坐标系的旋转。
这个问题在邱笑晨的一个pdf笔记里有过说明,主要意思是说对于一个四元数\(q=cos(\theta/2) + u^g . sin(\theta/2)\),我们一般将其表示为\(q_g^b\),其中g就是四元数中轴角表示的轴所在的参考系,b是经过当前四元数变换后一个向量所在的另一个参考系。因此按理来说应该需要有\(q_g^b\)与\(R_g^b\)(从g坐标系到b坐标系的旋转变换矩阵)相互映射的关系的。但是按照传统的右手规则定义的四元数不满足这个映射,而是满足\(q_g^b\)与\(R_b^g\)互为映射,因此shuster改变了四元数的虚部乘法规则,使用左手定则定义,获得的四元数刚好满足\(q_g^b\)与\(R_g^b\)互为映射。
5. BCH公式与伴随
在三维旋转矩阵群SO(3)上没有提供加法,因此不能求旋转矩阵的导数。但是三维旋转矩阵群对应的李代数与其是可以通过指数映射的(罗德里格斯公式),并且其李代数上是可以进行加法的,因此我们对姿态的更新通过流形进行更新。
BCH公式主要是
\[ R_1 R_2 = \textbf{exp}({\phi_1}^{\wedge})\textbf{exp}({\phi_2}^{\wedge}) \approx \begin{equation} \begin{cases} \textbf{exp}(( J_l(\phi_2)^{-1} \phi_1 + \phi_2 )^{\wedge}) & \textbf{if } \phi_1 \textbf{ is small}\\ \textbf{exp}(( J_r(\phi_1)^{-1} \phi_2+ \phi_1 )^{\wedge}) & \textbf{if } \phi_2 \textbf{ is small} \end{cases} \end{equation} \] 与 \[ \textbf{exp}((\phi_1+\phi_2)^{\wedge}) \approx \begin{equation} \begin{cases} \textbf{exp}( (J_l(\phi_2){\phi_1})^{\wedge}) \textbf{exp}({\phi_2}^{\wedge}) & \textbf{if } \phi_1 \textbf{ is small}\\ \textbf{exp}({\phi_1}^{\wedge}) \textbf{exp}( (J_r(\phi_1){\phi_2})^{\wedge}) & \textbf{if } \phi_2 \textbf{ is small} \end{cases} \end{equation} \]
在上面第2节中使用了第一个BCH公式。
伴随性质 \[ \mathbf{R}^T \exp \left(\boldsymbol{\phi}^{\wedge}\right) \mathbf{R} = \exp \left(\left(\mathbf{R}^{T} \boldsymbol{\phi}\right)^{\wedge}\right) \]
6. gps视觉插值残差姿态雅克比推导
本节主要是想完成一次对姿态的扰动求导,选取了gps视觉插值残差对相邻vio帧的姿态雅克比求导。此处残差构造可以参考黄国权老师的论文《Intermittent GPS-aided VIO: Online Initialization and Calibration》。
此处假设k时刻gnss的测量的时间戳在vio的a帧与b帧之间,因此首先会通过线性插值获得k时刻的imu位姿,此处主要分析姿态,因此姿态插值的公式为(可以发现系统使用JPL的姿态表示): \[ R_V^{k} = Exp(\lambda Log(R_V^b R_a^V))R_V^a \] 其中此处求导中最关键的就是此处k时刻的imu姿态对a时刻imu姿态的雅克比,与对b时刻imu姿态的雅克比的求导。 \[ \begin{aligned} \frac{\mathrm{d} Log \left(R_V^{k}\right)}{\mathrm{d} Log (R_V^b)} &=\lim _{\phi \rightarrow 0} \frac{Log \left(Exp(\lambda Log( Exp(\phi) R_V^b R_a^V))R_V^a \right)- Log \left(Exp(\lambda Log(R_V^b R_a^V))R_V^a \right)} {\phi} \\ &=\lim _{\phi \rightarrow 0} \frac{Log \left(Exp \left( \lambda J_l({\theta}_a^b)^{-1} \phi + \lambda {\theta}_a^b \right) R_V^a \right) - Log \left(Exp(\lambda {\theta}_a^b) R_V^a \right)}{\phi} \\ &=\lim _{\phi \rightarrow 0} \frac{Log \left(Exp \left( \lambda J_l(\lambda {\theta}_a^b) J_l({\theta}_a^b)^{-1} \phi \right) Exp \left(\lambda {\theta}_a^b \right) R_V^a \right) - Log \left(Exp(\lambda {\theta}_a^b) R_V^a \right)}{\phi} \\ &=\lim _{\phi \rightarrow 0} \frac{\lambda J_l(Log \left(Exp \left(\lambda {\theta}_a^b \right) R_V^a \right))^{-1} J_l(\lambda {\theta}_a^b) J_l({\theta}_a^b)^{-1} \phi + Log \left(Exp \left(\lambda {\theta}_a^b \right) R_V^a \right) - Log \left(Exp(\lambda {\theta}_a^b) R_V^a \right)}{\phi} \\ &=\lambda J_l({\theta}_V^k)^{-1} J_l(\lambda {\theta}_a^b) J_l({\theta}_a^b)^{-1} \end{aligned} \]
这是错的,为啥呢?可以参考第2节对于不可加因变量的绕动求导,对应的正确推导如下
自变量的扰动是左扰动(对b帧姿态的扰动),因变量的扰动是也是左扰动(我们探索对k帧姿态的扰动)
\[ \begin{aligned} \frac{\mathrm{d} Log \left(R_V^{k}\right)}{\mathrm{d} Log (R_V^b)} &=\lim _{\phi \rightarrow 0} \frac{Log \left(Exp(\lambda Log( Exp(\phi) R_V^b R_a^V))R_V^a \ \ \ \left(Exp(\lambda Log(R_V^b R_a^V))R_V^a \right)^{-1} \right)} {\phi} \\ &=\lim _{\phi \rightarrow 0} \frac{Log \left(Exp \left( \lambda J_l({\theta}_a^b)^{-1} \phi + \lambda {\theta}_a^b \right) R_V^a \ \ \ \left(Exp(\lambda {\theta}_a^b) R_V^a \right)^{-1}\right) }{\phi} \\ &=\lim _{\phi \rightarrow 0} \frac{Log \left(Exp \left( \lambda J_l(\lambda {\theta}_a^b) J_l({\theta}_a^b)^{-1} \phi \right) Exp \left(\lambda {\theta}_a^b \right) R_V^a \ \ \ \left(Exp(\lambda {\theta}_a^b) R_V^a \right)^{-1} \right)}{\phi} \\ &=\lim _{\phi \rightarrow 0} \frac{Log \left(Exp \left( \lambda J_l(\lambda {\theta}_a^b) J_l({\theta}_a^b)^{-1} \phi \right) \right)}{\phi} \\ &=\lambda J_l(\lambda {\theta}_a^b) J_l({\theta}_a^b)^{-1} \end{aligned} \]
利用第2节的方式会更简单
\[ \begin{aligned} Exp(\theta) Exp(\lambda Log(R_V^b R_a^V) )R_V^a &= Exp(\lambda Log( Exp(\phi) R_V^b R_a^V) )R_V^a \\ Exp(\theta) Exp(\lambda {\theta}_a^b ) &= Exp ( \lambda J_l({\theta}_a^b)^{-1} \phi + \lambda {\theta}_a^b ) \\ Exp(\theta) Exp(\lambda {\theta}_a^b ) &= Exp \left( \lambda J_l(\lambda {\theta}_a^b) J_l({\theta}_a^b)^{-1} \phi \right) Exp \left(\lambda {\theta}_a^b \right) \\ Exp(\theta) &= Exp \left( \lambda J_l(\lambda {\theta}_a^b) J_l({\theta}_a^b)^{-1} \phi \right) \end{aligned} \]