dijkstra算法和astar算法

图搜索算法

图搜索算法指在一个类似图的数据结构上进行路径搜索的算法的总称。二维网格地图其实就是一种类似图的数据结构，每个网格代表一个图节点，它连接着自身周围的四个相邻网格（图节点）。

可以将图搜索的图结构转换成搜索树结构。那么最具代表性的两类图搜索算法就是深度优先与广度优先算法。

需要提前强调的一点是，为了不会形成环路，已经访问过的节点需要做标记，并且不再访问。

深度优先算法-Deep First Search

可以使用栈（先进后出）这种数据结构来实现。

dfs

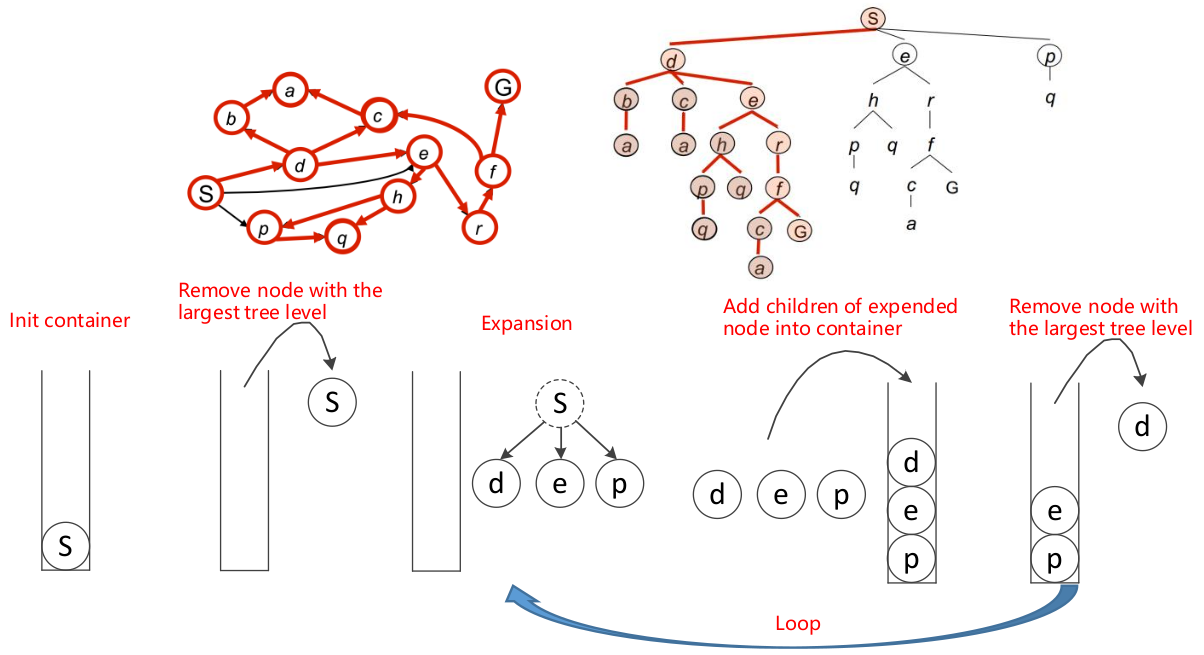
可以使用栈结构实现，几乎不太可能找到最优解，因此更短的路径大部分没有试过。因此dfs算法实现简单、路径可能不是最优解、寻路时间比较长

广度优先算法-Breadth First Search

可以使用队列（先进先出）这种数据结构来实现。

bfs

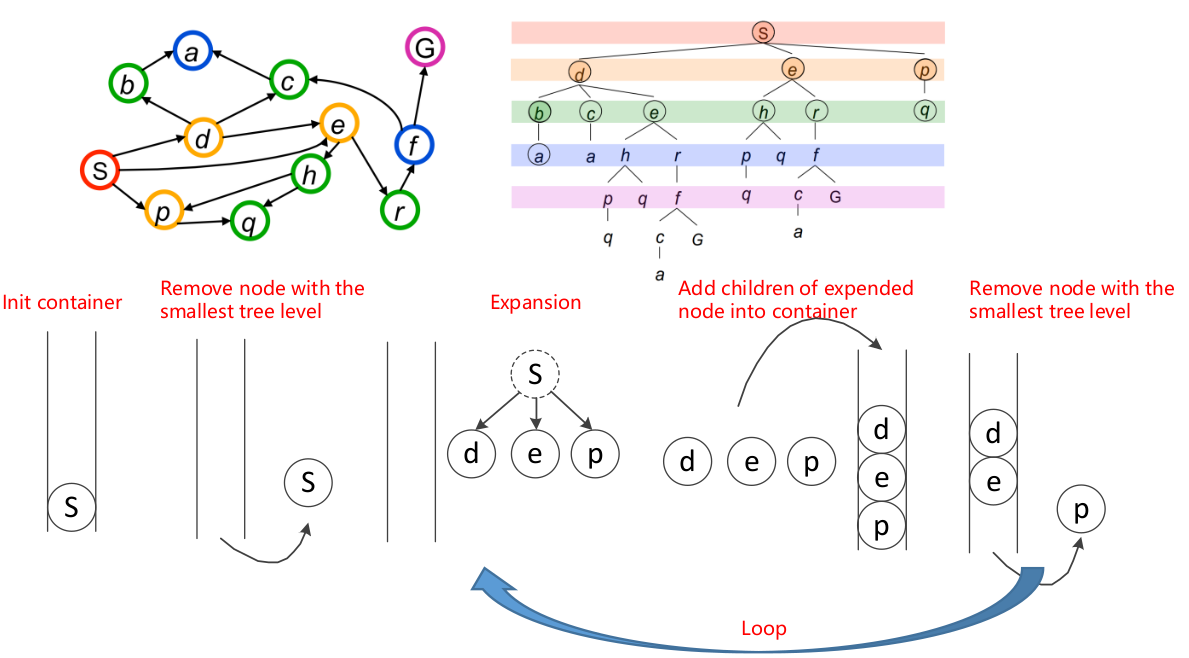
可以使用队列结构实现，由于是逐层遍历的，因此遍历到目标点时肯定可以得到一条最短路径，因此更短的所有路径都已经遍历了，不能到达目标点。因此BFS算法实现简单、路径能找到最优解、算法消耗时间比较大、遍历的点有点多。

启发式搜索

传统的广度优先搜索与深度优先搜索它们本质的区别就是每次从当前集合中弹出要读取的节点的规则，BFS是先入先出，使得每次弹出搜索树上深度最小的节点；DFS是先入后出，使得每次弹出搜索树上深度最大的节点；这两种弹出规则下两种方法的优缺点都很明显，并且都没有利用目标节点位置信息。因此后来为了找到一种更优的图搜索算法，就有了启发式搜索算法，启发式搜索算法简单来说就是指根据目标位置人为定义的另一种更合理的规则来弹出集合中的节点，这种规则就是所谓的启发。

最简单的启发式搜索算法就是贪心算法。贪心算法的启发规则就是简单的弹出当前集合中距离终点最近的那个节点。当然实际的距离我们是不会提前知道的（虽然一般我们知道起点和终点的位置，但是我们不知道地图或者地图会变化），所以用来做启发的是一种理想中的距离，比如假设没有障碍物的存在，使用欧式（或曼哈顿等）距离来做启发。

其实上述的广度优先与深度优先还有一个缺点，那就是只能在无权图上做规划，因为是以生成树上节点的深度来启发的。

Dijkstra算法

算法要点：

• 弹出规则：g(n)-对于一个节点n，g(n)表示从起点到当前节点已经耗费的总代价。（Dijkstra算法每次弹出g(n)最小的那个节点，其实类似BFS，BFS的g(n)为节点在搜索树上的深度）
• 更新规则：对于当前节点n的一个邻居节点m，如果m已经在当前集合中，则根据当前路径（n->m）重新确定一个g(m)，如果其小于原本的值，则对g(m)进行更新。

算法伪代码：

Initial初始化: 初始节点g(X_s)=0,其他所有节点g(n)=infinite;设计一个数据结构priority queue(自动对其中数据根据g(n)进行排序) 
Loop:
	- if the queue is empty, return FALSE; break;
	- Remove the node "n" with the lowest g(n) from the queue
	- Mark node "n" as expanded
	- if the node "n" is the goal state, return TRUE; break;
	- For all unexpanded neighbors "m" of node "n"
		- if g(m)=infinite
			- g(m) = g(n) + Cnm
			- Push node "m" into the queue
		- if g(m) > g(n) + Cnm
			- g(m) = g(n) + Cnm
	- end
End Loop	

Dijkstra

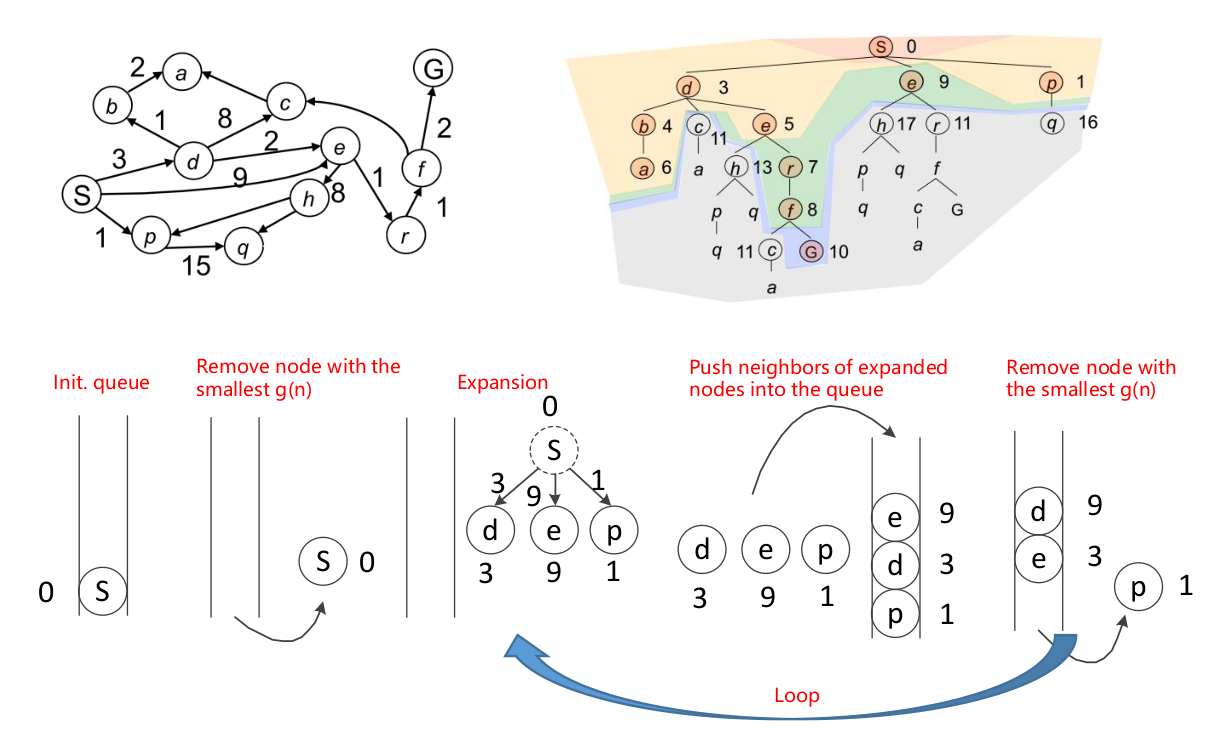
优点：完备的，只要有解一定可以找到最优解。缺点：只利用了到目前为止的成本，没有利用目标位置的信息，这也导致了当图中每条边权重相同时，Dijkstra算法也就退化成了广度优先搜索算法。所以本算法其实就是对BFS的拓展使其可以用于有权图搜索。此类算法盲目穷举进行探索的，都不是启发式搜索算法。

• 在cpp中上述Priority queue可以使用下面三种方式实现
  • std::priority_queue
  • std::make_heap
  • std::mutimap

A-star算法

算法要点：

• 累积成本函数g(n): 从起点到当前节点n累积的成本cost；
• 启发函数h(n): 从当前节点n到目标估计成本cost（类似欧式距离、曼哈顿距离等）；
• 估计成本函数 f(n) = g(n) + h(n): 经过当前节点n从起始节点到目标节点的估计成本；
• 策略：每次弹出f(n)最小的节点
  • 更新策略：对于当前节点n的一个邻居节点m，如果m已经在当前集合中，则根据当前路径（n->m）重新确定一个g(m)，如果其小于原本的值，则对g(m)进行更新。
  • 每个被访问（弹出）过的节点n，一定找到了从起点到n的一个最短路径

算法伪代码：

Initial初始化: 初始节点g(X_s)=0,其他所有节点g(n)=infinite;初始化所有节点h(n);设计一个数据结构priority queue(自动对其中数据根据g(n)进行排序) 
Loop:
	- if the queue is empty, return FALSE; break;
	- Remove the node "n" with the lowest f(n) from the queue
	- Mark node "n" as expanded
	- if the node "n" is the goal state, return TRUE; break;
	- For all unexpanded neighbors "m" of node "n"
		- if g(m)=infinite
			- g(m) = g(n) + Cnm
			- Push node "m" into the queue
		- if g(m) > g(n) + Cnm
			- g(m) = g(n) + Cnm
	- end
End Loop	

astar

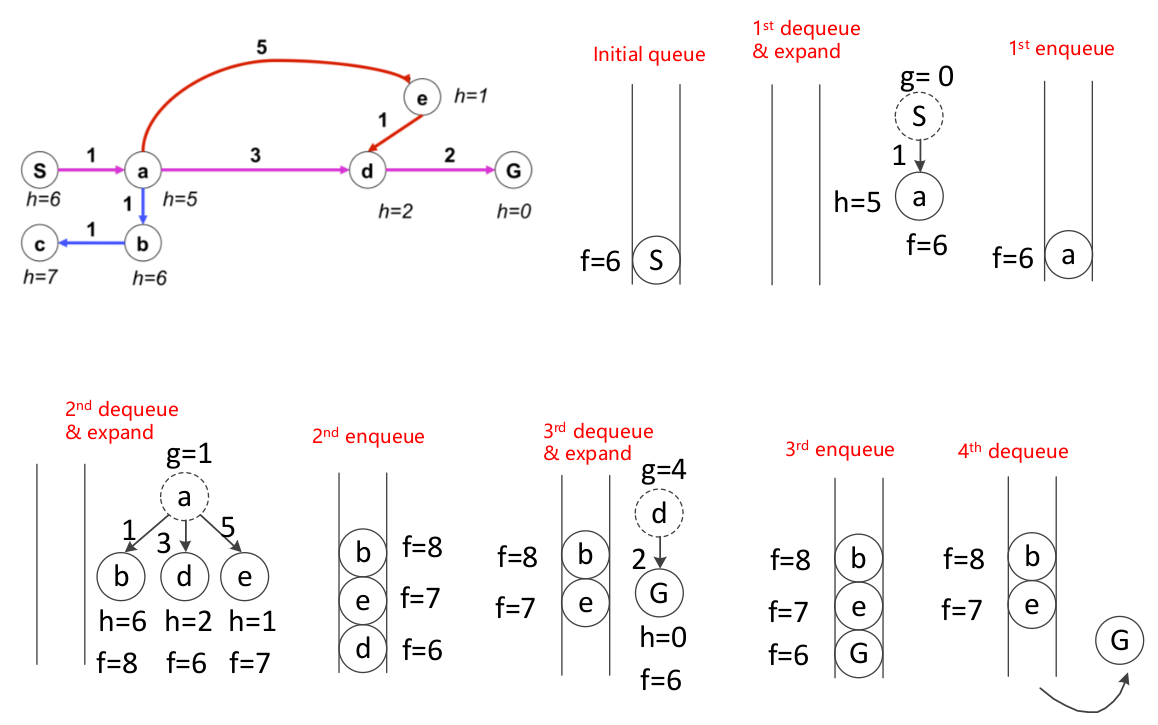
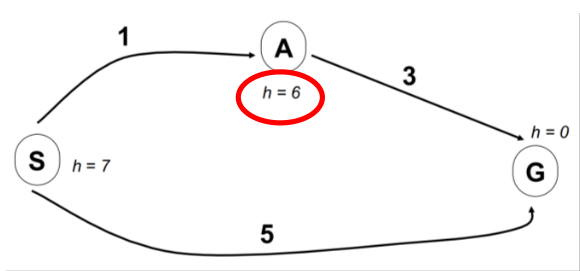
由于引入了启发函数h，如果启发函数不合理，A星算法有可能是找不到最优解的（如下图）。如果想保证a星算法可以找到最优解，需要满足任意 h(n)小于等于节点n到终点的实际cost。

astar_wrong

• 加权A星算法，即使用的\(f(n)=g(n)+\varepsilon h(n)\)，当\(\varepsilon >1\)时，代表着增加了h(n)的权重，这有可能导致不能得到最优解，但是可以更快的到达目标（有可能提升几十倍 ）。
  • 这种方法其实是一种 最优性 vs 速度（贪心算法肯定是最快的，只是不能得到最优解）；
  • 已经被证明：\(cost_{solution} \le \varepsilon cost_{optimal}\)，即结果的cost与最优解的cost的关系；

如果想查看不同算法的动态效果，这个网页提供了在线模拟运行的小程序。

• 常识强调：
  • openlist：也就是维护的priority queue，也就是所有已经扩展过的节点的邻居（不包括已经扩展过的节点）组成的容器；
  • closelist: 也就是已经扩展过（访问过）的节点组成的容器；

参考文献

• [1] 深蓝学院运动规划课程PPT（高飞老师）。