自监督学习备忘
目录
以下转载自知乎的一篇文章
自监督学习(self-supervised learning)可以被看作是机器学习的一种“理想状态”,模型直接从无标签数据中自行学习,无需标注数据。本文主要对当前自监督学习涉及到的一些方面进行总结(笔记)。
自监督学习简介
- 自监督学习的核心,在于如何自动为数据产生标签。例如输入一张图片,把图片随机旋转一个角度,然后把旋转后的图片作为输入,随机旋转的角度作为标签。再例如,把输入的图片均匀分割成3*3的格子,每个格子里面的内容作为一个patch,随机打乱patch的排列顺序,然后用打乱顺序的patch作为输入,正确的排列顺序作为label。类似这种自动产生的标注,完全无需人工参与。
- 自监督学习如何评价性能?自监督学习性能的高低,主要通过模型学出来的feature的质量来评价。feature质量的高低,主要是通过迁移学习的方式,把feature用到其它视觉任务中(分类、分割、物体检测...),然后通过视觉任务的结果的好坏来评价。目前没有统一的、标准的评价方式。
- 自监督学习的一个研究套路。前面说到,自监督学习的核心是如何给输入数据自动生成标签。之前的很多工作都是围绕这个核心展开的。一般的套路是:首先提出一个新的自动打标签的辅助任务(pretext task,例如:旋转图片、打乱patch顺序),用辅助任务自动生成标签,然后做实验、测性能、发文章。每年都有新的辅助任务被提出来,自监督学习的性能也在不断提高,有的甚至已经接近监督学习的性能。总体上说,或者是提出一种完全新的辅助任务,或者是把多个旧的辅助任务组合到一起作为一个“新”的辅助任务。
以下转载自另一篇知乎文章
自监督学习与监督学习和无监督学习的比较
手动数据注释是监督学习中必不可少的步骤,这是耗时,费力且有噪声的。与有监督的方法不同,无监督的方法不依赖于人类注释,并且通常集中在数据良好表示(例如平滑度,稀疏性和分解)的预设先验上。无监督方法的经典类型是聚类方法,例如高斯混合模型,它将数据集分解为多个高斯分布式子数据集。然而,非监督学习学习由于预设先验的一般性较差而不太值得信赖,在某些数据集(例如非高斯子数据集)上选择将数据拟合为高斯分布可能是完全错误的。
自我监督方法可以看作是一种具有监督形式的特殊形式的非监督学习方法,这里的监督是由自我监督任务而不是预设先验知识诱发的。与完全不受监督的设置相比,自监督学习使用数据集本身的信息来构造伪标签。在表示学习方面,自我监督学习具有取代完全监督学习的巨大潜力。人类学习的本质告诉我们,大型注释数据集可能不是必需的,我们可以自发地从未标记的数据集中学习。更为现实的设置是使用少量带注释的数据进行自学习。这称为Few-shot Learning。
在自监督学习中,如何自动获取伪标签至关重要。 根据伪标签的不同类型,我将自我监督的表示学习方法分为4种类型:基于数据生成(恢复)的任务,基于数据变换的任务,基于多模态的任务,基于辅助信息的任务。
第一类-基于数据生成的任务
对于第一种类型,其实自监督学习与非监督学习本质上是基本相同的。所有的非监督学习方法,例如数据降维(PCA:在减少数据维度的同时最大化的保留原有数据的方差),数据拟合分类(GMM: 最大化高斯混合分布的似然), 本质上都是为了得到一个良好的数据表示并希望其能够生成(恢复)原始输入。这也正是目前很多的自监督学习方法赖以使用的监督信息。基本上所有的encoder-decoder模型都是以数据恢复为训练损失。
自监督学习的出发点是考虑在缺少标签或者完全没有标签的情况下,依然学习到能够表示原始图片的良好有意义的特征。那么什么样的特征是良好有意义的呢?在第一类自监督任务——数据恢复任务中,能够通过学习到的特征还原生成原始数据的特征,我们认为是良好有意义的。看到这里,实际上大家能够联想到自动编码器类的模型,甚至更简单的PCA。实际上,几乎所有的非监督学习方法都是以这个原则作为基础的。包括非常火的GAN
GAN的核心是通过Discriminator去缩小Generator distribution和real distribution之间的距离。GAN的学习过程不需要人为进行数据标注,其监督信号也即是优化目标就是使得上述对抗过程趋向平稳。
这里我们以两篇具体的paper为例子,介绍数据恢复类的自监督任务如何操作实现。我们的重点依然是视觉问题,这里分别介绍一篇图片上色的文章和一篇视频预测的文章。其余的领域比如NLP,其本质是类似的,在弄清楚了数据本身的特点之后,可以先做一些低级的照猫画虎的工作。
上色任务
设计自监督任务时需要一些巧妙的思考。比如图片色彩恢复任务,我们已有的数据集是一张张的彩色图片,假如去掉色彩,作为感性思考者的我们,是否能够从黑白图片中显示的内容推测原来图片真实的色彩?对于一个婴儿来说可能很难,但是对于我们来说,生活的经历告诉我们瓢虫应当是红色的(下图第二行中)。我们是如何做出预测的?事实上,我们通过观察大量的瓢虫,在脑中建立了从“瓢虫”到“红色”的映射。
把这个学习过程推广到我们的模型上,在给定黑白输入的情况下,我们用正确的彩色的原始图像作为学习的标签,从而模型会试着理解原始黑白图像中“每个区域”是“什么”进而去建立从是“什么”到“不同颜色”的映射。
当我们完成训练,模型的中间层feature map就得到了类似人脑对于“瓢虫”以及其他物体的记忆,以向量的形式。
视频预测——下一秒你会在哪里?
一般来说,视觉问题分成图片和视频两大类,图片数据可以认为具有i.i.d特性,而视频是由多个图片帧构成的,可以认为具有一定的Markov dependency,时序关系是他们之间最大的不同。比如最简单的思路,利用CNN提取单张图片特征可以做图片分类,再加入一个RNN或者LSTM去刻画Markov Dependency,便可以应用到视频上。
视频预测任务十分的耿直。怎么形容呢,他就是那种,你知道的,我们说视频中帧与帧之间存在时空连续性。类似的,人类会利用这种帧与帧之间的连续性,当我们看电影时突然按了暂停,下一秒下几秒会发生什么实际上我们是可以预测的。
同样,把这个学习过程推广到我们的模型上,在给定前一帧或者前几帧的情况下,我们用后续的视频帧作为学习的标签,从而模型会试着理解给定视频帧中的语义信息(发生了啥?)进而去建立从当前到未来的映射关系。
第二类-基于数据变换的任务
这种类型的自监督学习是大家熟知的窄意的自监督学习。本文链接
用一句话说明这一类任务,事实上原理很简单。对于样本 X ,我们对其做任意变换 T(X)=Y ,则自监督任务的目标是能够对生成的 Y 估计出其变换 T。下面介绍一种原理十分简单但是目前看来非常有效的自监督任务——Rotation Prediction。
给定输入图片 X ,我们对其做4个角度的旋转,分别得到 \(X_0, X_1, X_2, X_3\) ,并且我们知道其对应的变换角度分别为 0°,90°,180°,270° 。此时,任务目标即是对于以上4张图片预测其对应的旋转角度,这里每张图片都经过同样的卷积神经网。
我始终坚持的观点是自监督学习需要动机明确,这里我们能做的任意变换应当是对目标有益的。比如在Rotation Prediction中,作为人类的我们只有在理解了图片中是一只鸟站在枝头之后才知道X_0的旋转角度应当是 0° 。那么我们有理由相信,当模型能够做出同样正确的判断时,其中间的feature map必然携带了有意义的图片语义信息。
第三类-基于多模态数据的自监督任务
下面介绍一种典型的多模态数据,是的,你没有猜错,就是伴随声音信息的视频数据。我们平时看到的短视频,电影实际上都属于这一类多模态数据。基于多模态数据进行自监督学习其内含的假设是,视频每一帧的内容与对应的音轨应当存在相关性,比如在一段乐器演奏视频中,人类能够通过观察乐器的种类在脑海中想象出不同的音色(当然我并不懂乐器),同样的,在听到一段旋律的时候,人类能够通过已有的知识判断出这是来自那种乐器(当然我也并不能)。
本篇论文链接
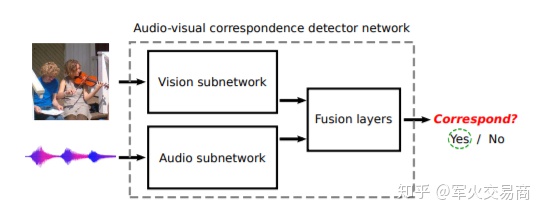
文中将此任务命名为Audio-Visual Correspondence Task,后文简称为AVC。AVC任务事实上是一个简单的二进制分类:针对每一个视频帧和一段音频剪辑,网络需要判断其是否彼此对应。对应的(正)对是在同一时间从同一视频,但从不同视频中提取了不匹配的(负)对。为了解决这个任务,我们期望模型能够学会在视觉和音频领域中检测各种语义概念。
应当指出,这项任务非常困难。模型需要从0开始建立网络以学习视觉和音频功能,并且却从未见过一个标签。此外,原始的视频数据可能非常嘈杂,音频源不一定在视频中可见(例如,摄像机操作员讲话,对视频进行旁白的人,声源不可见或被遮挡等),以及音频和视觉内容可能是完全不相关的(例如,带有附加音乐的视频,声音很小,周围环境诸如风之类的声音主导了音轨等)。
尽管如此,本文的结果仍然表明AVC网络能够相当成功地解决AVC任务,并且在此过程中习得非常好的视觉和听觉表示。
对比学习
说到当下最火热的非监督学习方法,非对比学习(Contrastive Learning)莫属。Bengio和Lecun在AAAI还是哪个会上力挺自监督学习尤其是对比学习方法,这篇简单介绍以下对比学习是为何物。
就我而言,当下的对比学习框架与之前的两篇文章(Exemplar learning)有着类似的思路,有兴趣大家可以自行阅读,在那两篇文章中,每一张图片被视为一个独立的class,我们对每一张图片做各种变换进行数据augmentation,这样就得到了一个多分类问题(有多少张图片就有多少个类别)。
对比学习可以视为将上面两篇文章中的Cross-entropy loss替换为contrastive loss之后的版本。我们用一个简单的例子描述对比学习:
假如有两张图片A(足球),B(猫咪),由于是非监督学习,我们并不知道真实标签,但我们知道A 和B分属不同的语义类别,即使我们对A和B分别做一些变换,比如旋转(R),裁减(C),高斯模糊(G)等等,在理想的情况下,人们仍然能够合理的避免变换的影响,将变换后的图片正确归类到A或是B。这一点很好理解,正常人都不会因为一张猫咪照被翻转之后就认为他变成了狗甚至是足球。
基于以上的动机,假设我们有模型f,我们希望f同样具有以上能力,假如我们用特征之间的距离来表示图片之间的关联度,那么分别图片A和图片B,我们希望旋转后的图片A与裁减后的图片后距离较近,而与高斯模糊后的图片B较远。
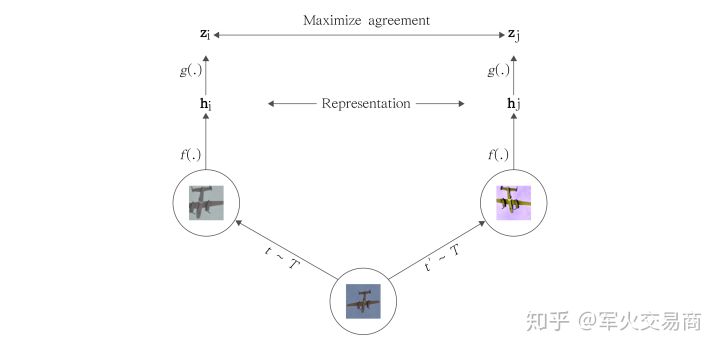
\[\operatorname{dist}(f(R(A)), f(C(A)))<\operatorname{dist}(f(R(A)), f(G(B)))\]
看到这里,有经验的同学可能会想到Triplet Loss,事实上我认为这两者确实蛮相似的,唯一的区别可能是这里的负样本不是一对,而是很多对,也即,在满足上式的同时,对于图片A和数据库中的其他图片,我们都希望其满足此距离关系:
\[\operatorname{dist}(f(R(A)), f(C(X)))<\operatorname{dist}(f(R(A)), f(G(X))), \quad X \in R^{H \times W}\]
大家思考一下,实际上最终的目标是,希望每一张图片及其变换后的图片所产生的特征形成一个cluster,在我们假设类内方差小于类间方差的情况下,这一点是可以保证的。