BA优化中Jacobian矩阵的计算
之前写过一篇讲解BA的博客,不过那篇主要侧重于讲解BA在slam中的应用与求解方式,但是忽略了对于细节的边的构造与jacobian矩阵的计算的讲解,前几天有人提醒我这一点,所以今天抽出来时间补充一下。
BA优化中的边(重投影误差)
Bundle Adjustment,中文翻译有捆集调整、光束法平差。它的主要思想是最小化重投影误差。
BA优化的误差边也就是重投影误差边。 - 投影过程是将一个地图点(三维坐标为\((X,Y,Z)\))投影到当前帧(假设位姿为\(T_{wc}\))的像素平面上(得到投影坐标为\((u,v)\))
- 误差边的定义是测量坐标(该帧上提取到的此地图点的位置\((u_m,v_m)\))减去投影得到坐标\((u,v)\)
\[ e = [u_m,v_m]^T - [u,v]^T \]
BA优化中的节点(投影点与关键帧)
通常我们最经常放入BA中进行优化的节点有两个 1. 地图点的三维坐标为\((X,Y,Z)\)
- 被投影帧的位姿\(T_{wc}\)
当然了,BA优化时只要观测到的约束足够多,方程就足够多,因此可以优化更多节点。比如我们还可以放入的节点有相机内参等。
jacobian的推导
前面已经列出来了重投影误差的定义为:
\[ e = [u_m,v_m]^T - [u,v]^T \]
然后被投影帧的位姿为\(T_{wc}\),地图点在世界坐标系中的位置为\(P\),则将其变换到该帧的相机坐标系下的坐标为
\[ P' = T_{wc} * P = [X', Y', Z']^T\]
然后将这个点投影到像素平面上的操作为(此处为了简单忽略了相机畸变)
\[ \left[\begin{array}{c}{Z' u} \\ {Z' v} \\ {Z'}\end{array}\right]=\left[\begin{array}{ccc}{f_{x}} & {0} & {c_{x}} \\ {0} & {f_{y}} & {c_{y}} \\ {0} & {0} & {1}\end{array}\right]\left[\begin{array}{c}{X^{\prime}} \\ {Y^{\prime}} \\ {Z^{\prime}}\end{array}\right] \]
即
\[ u=f_{x} \frac{X^{\prime}}{Z^{\prime}}+c_{x}, \quad v=f_{y} \frac{Y^{\prime}}{Z^{\prime}}+c_{y} \]
重投影误差对地图点三维坐标的jacobian
由上,我们首先计算重投影误差对地图点相机坐标系下坐标\(P^{\prime}\)的偏导,
\[ \frac{\partial e}{\partial P^{\prime}}=-\left[\begin{array}{ccc}{\frac{\partial u}{\partial X^{\prime}}} & {\frac{\partial u}{\partial Y^{\prime}}} & {\frac{\partial u}{\partial Z^{\prime}}} \\ {\frac{\partial v}{\partial X^{\prime}}} & {\frac{\partial v}{\partial Y^{\prime}}} & {\frac{\partial v}{\partial Z^{\prime}}}\end{array}\right]=-\left[\begin{array}{ccc}{\frac{f_{x}}{Z^{\prime}}} & {0} & {-\frac{f_{x^{\prime}} X^{\prime}}{Z^{\prime 2}}} \\ {0} & {\frac{f_{y}}{Z^{\prime}}} & {-\frac{f_{y} Y^{\prime}}{Z^{\prime 2}}}\end{array}\right] \]
接着根据如下链式法则与坐标变换关系
\[ \frac{\partial e}{\partial \boldsymbol{P}}=\frac{\partial \boldsymbol{e}}{\partial \boldsymbol{P}^{\prime}} \frac{\partial \boldsymbol{P}^{\prime}}{\partial \boldsymbol{P}} \]
\[ \boldsymbol{P}^{\prime} = \boldsymbol{R} \boldsymbol{P} + t \]
可以得到最终的重投影误差对地图点三维坐标的jacobian
\[ \frac{\partial e}{\partial \boldsymbol{P}} = -\left[\begin{array}{ccc}{\frac{f_{x}}{Z^{\prime}}} & {0} & {-\frac{f_{x^{\prime}} X^{\prime}}{Z^{\prime 2}}} \\ {0} & {\frac{f_{y}}{Z^{\prime}}} & {-\frac{f_{y} Y^{\prime}}{Z^{\prime 2}}}\end{array}\right] \boldsymbol{R} \]
重投影误差对被投影帧位姿的jacobian
此处需要说明的是,对于位姿变换(对应的李群是\(SE(3)\))的求导我们一般将其变换到\(SE(3)\)对应的李代数\(\xi\)上使用扰动模型来求导。
根据前面的推导我们可以发现,重投影误差项\(e\)中与位姿\(T_{wc}\)相关的只有\(\boldsymbol{P}^{\prime}\),因此可以将求解过程分解为如下两步
\[ \frac{\partial e}{\partial \delta \xi}=\frac{\partial e}{\partial P^{\prime}} \frac{\partial P^{\prime}}{\partial \delta \xi} \]
其中第一部分\(\frac{\partial e}{\partial P^{\prime}}\)在前面已经求解出来了,第二部分可以通过使用扰动模型左乘扰动量来求得(具体步骤见附录1)
\[ \frac{\partial(\boldsymbol{T} \boldsymbol{P})}{\partial \delta \boldsymbol{\xi}}=(\boldsymbol{T} \boldsymbol{P})^{\odot}=\left[\begin{array}{cc}{\boldsymbol{I}} & {-\boldsymbol{P}^{\prime \wedge}} \\ {\boldsymbol{0}^{\mathrm{T}}} & {\boldsymbol{0}^{\mathrm{T}}}\end{array}\right] \]
由于上面是使用的\(\boldsymbol{P}\)的齐次坐标形式,所以从上式结果中取出前三维就是(这是一个\(3*6\)大小的矩阵)
\[ \frac{\partial \boldsymbol{P}^{\prime}}{\partial \delta \boldsymbol{\xi}}=\left[\boldsymbol{I},-\boldsymbol{P}^{\prime \wedge}\right] \]
然后将两项相乘就可以得到我们想要的结果--重投影误差对被投影帧位姿的jacobian
\[ \frac{\partial e}{\partial \delta \xi}=-\left[\begin{array}{lllll}{\frac{f_{x}}{Z^{\prime}}} & {0} & {-\frac{f_{x} X^{\prime}}{Z^{\prime 2}}} & {-\frac{f_{x} X^{\prime} Y^{\prime}}{Z^{\prime 2}}} & {f_{x}+\frac{f_{x} X^{2}}{Z^{\prime 2}}} & {-\frac{f_{x} Y^{\prime}}{Z^{\prime}}} \\ {0} & {\frac{f_{y}}{Z^{\prime}}} & {-\frac{f_{y Y^{\prime}}}{Z^{\prime 2}}} & {-f_{y}-\frac{f_{y} Y^{\prime 2}}{Z^{\prime 2}}} & {\frac{f_{y} X^{\prime Y^{\prime}}}{Z^{\prime 2}}} & {\frac{f_{y} X^{\prime}}{Z^{\prime}}}\end{array}\right] \]
附录1
假设如下求导中的左乘的扰动项的李代数为\(\delta \boldsymbol{\xi}=[\delta \boldsymbol{\rho}, \delta \phi]^{\mathrm{T}}\),那么:
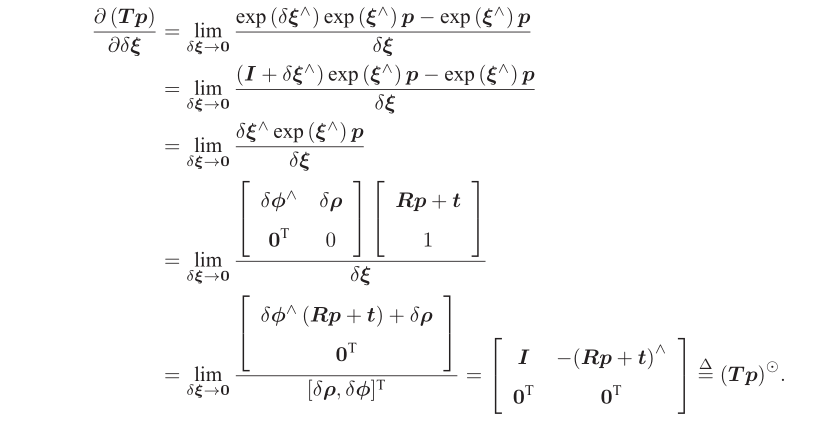
上面最后一行矩阵除法,与矩阵乘法规则类似,只是乘号变成了除号。其使用一个\(4×1\)矩阵除以一个\(1×6\)矩阵得到一个\(4×6\)矩阵
附录2
雅克比矩阵即是偏导数矩阵,由于一般待求导的目标函数的因变量是列向量,自变量也是列向量,在求雅克比矩阵时遵循如下规则:
\[ \frac{\mathrm{d}\left[\begin{array}{l}{a} \\ {b}\end{array}\right]}{\mathrm{d}\left[\begin{array}{l}{x} \\ {y}\end{array}\right]}=\left[\begin{array}{cc}{\frac{\mathrm{d} a}{\mathrm{d} x}} & {\frac{\mathrm{d} a}{\mathrm{d} y}} \\ {\frac{\mathrm{d} b}{\mathrm{d} x}} & {\frac{\mathrm{d} b}{\mathrm{d} y}}\end{array}\right] \]
其实只需要明确一点,上述公式便很容易记起来了。对于输入为n维向量,输出为m维向量的变换(即从\(R^n\)到\(R^m\)的变换),它的雅克比矩阵为\(m*n\)维。即行数由输出向量的维度决定,列数由输入向量的维度决定
参考文献
- [1] 视觉slam十四讲 从理论到实践 高翔等著;