dogleg算法解析

之前有仔细介绍过非线性优化，其中二阶梯度的方法有高斯牛顿法、LM算法、dogleg算法等。前段时间仔细研究了dogleg算法的实现步骤，今天抽出时间总结一下。

dogleg属于二阶梯度法，为了解决高斯牛顿法在使用一阶导数平方近似计算hessian矩阵时可能不准确的问题，它结合了高斯牛顿法与最速下降法，通过定义近似半径来限制近似的可执行范围。本质上与LM算法类似，不过实现细节大有不同。

算法

dogleg的思想很简单，对于一个非线性优化问题，它的每次的迭代步骤可以归纳如下：

1. 首先计算当前其高斯牛顿方法的迭代步长\(H_{gn}\)，然后计算最速下降法的迭代步长\(H_{sd}\)。

2. 根据第一步中确定的\(H_{gn}\)与\(H_{sd}\)相对与当前信赖域半径\(r\)的大小确定本次dogleg更新的步长\(\delta\)；

3. 使用第二步中确定的更新步长进行更新，然后计算\(\rho\)（与LM中相同），根据其大小判断是否执行本次迭代与如何更新信赖域半径\(r\)。

第一步

第一步是计算高斯牛顿与最速下降两种方法的更新步长。

• 高斯牛顿法步长\(H_{gn}\)可以通过求解如下方程组得到（推导可见非线性优化）

\[\left(\mathbf{J}(\mathbf{x})^{\top} \mathbf{J}(\mathbf{x})\right) \mathbf{h}_{\mathrm{gn}}=-\mathbf{J}(\mathbf{x})^{\top} \mathbf{f}(\mathbf{x}) \]

• 最速下降法步长\(H_{sd}\)，获得可以分为两步来获得
  • 第一步是先获得最速下降的方向
  • 第二步是确定最速下降的步长
  • 最后综合方向与步长即可得到更新的向量

首先，最速下降法的方向即是梯度反方向，先不考虑模长，我们可以使用下面公式表示(其中ｇ表示梯度方向)

\[ \mathbf{h}_{\mathrm{sd}} = -\mathbf{g} = -\mathbf{J}(\mathbf{x})^{\top} \mathbf{f}(\mathbf{x}) \]

然后我们知道利用雅克比矩阵可以得到下面模型：

\[ \begin{aligned} \mathbf{f}\left(\mathbf{x}+\alpha \mathbf{h}_{\mathrm{sd}}\right) & \simeq \mathbf{f}(\mathbf{x})+\alpha \mathbf{J}(\mathbf{x}) \mathbf{h}_{\mathrm{sd}} \\ F\left(\mathbf{x}+\alpha \mathbf{h}_{\mathrm{sd}}\right) & \simeq \frac{1}{2}\left\|\mathbf{f}(\mathbf{x})+\alpha \mathbf{J}(\mathbf{x}) \mathbf{h}_{\mathrm{sd}}\right\|^{2} \\ &=F(\mathbf{x})+\alpha \mathbf{h}_{\mathrm{sd}}^{\top} \mathbf{J}(\mathbf{x})^{\top} \mathbf{f}(\mathbf{x})+\frac{1}{2} \alpha^{2}\left\|\mathbf{J}(\mathbf{x}) \mathbf{h}_{\mathrm{sd}}\right\|^{2} \end{aligned} \]

我们对上述模型求最小值（对\(\alpha\)求导并另导数为0），此时\[\alpha\]应取值为：

\[ \alpha=-\frac{\mathbf{h}_{\mathrm{sd}}^{\top} \mathbf{J}(\mathbf{x})^{\top} \mathbf{f}(\mathbf{x})}{\left\|\mathbf{J}(\mathbf{x}) \mathbf{h}_{\mathrm{sd}}\right\|^{2}}=\frac{\|\mathbf{g}\|^{2}}{\|\mathbf{J}(\mathbf{x}) \mathbf{g}\|^{2}} \]

所以，最后最速下降法的更新向量为

\[ \mathbf{h}_{\mathrm{sd}} = \alpha \mathbf{h}_{\mathrm{sd}} \]　

第二步

通过当前的信赖域半径与上一步计算的两种步长结合计算处dogleg算法的更新步长更新规则如下：

dogleg

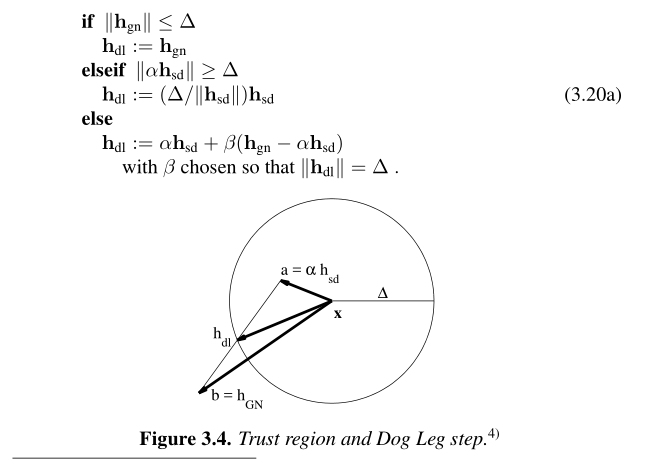
上图中的更新规则描述的较为清楚，但是代码实现尚有难度，主要是\(\beta\)的值较难确定。我在网上看到了一个更加明确的规则，将上述更新规则总结为一个统一的表达式。

\[ h_{dl}=\left\{\begin{array}{ll}{\tau h_{sd},} & {0 \leq \tau \leq 1} \\ {h_{sd}+(\tau-1)\left(h_{gn}-h_{sd}\right),} & {1 \leq \tau \leq 2}\end{array}\right. \]

可以发现dogleg的更新向量是在最速下降法与高斯牛顿法之间变换，并且最终的更新向量会小于等于信赖域半径。

其中比较关键的是变量\(\tau\)的确定，我直接贴出代码(其中delta_ \(\delta\)是信赖区域的半径大小)

double tau;
if(H_gn.norm() <= delta_)
    tau = 2;
else if(H_sd.norm() >= delta_)
    tau = delta_ / H_sd.norm() ;
else{
    VecX tmp = H_gn - H_sd ;
    tau = (- H_sd.transpose() * tmp + sqrt(pow((H_sd.transpose() * tmp),2) - tmp.squaredNorm() * (H_sd.squaredNorm() - pow(delta_,2)))) / tmp.squaredNorm()       ;
    tau += 1;     
}

第三步

判断改更新是否执行，并更新信赖域半径，此处的迭代策略比较简单，我是看的参考文献第一篇提供的策略，直接贴代码了。

注意此处有个\(\rho\)的计算，其值为

\[ \rho=\frac{F(\mathbf{x})-F\left(\mathbf{x}+\Delta \mathbf{x}_{\operatorname{dl}}\right)}{L(\mathbf{0})-L\left(\Delta \mathbf{x}_{\mathrm{dl}}\right)} \]

其中分母是此次更新后真实目标函数损失减少的量，分子是使用近似模型此次更新后目标函数损失应该减少的量。其中\(L(h)\)函数是如下线性函数模型

\[L(\mathbf{h}) = \frac{1}{2}\|\mathbf{f}(\mathbf{x})+\mathbf{J}(\mathbf{x}) \mathbf{h}\|^{2}\]

// 狗腿
bool Problem::IsGoodStep() {
    //此处是计算当前目标函数的损失
    double tempChi = 0.0;
    for(auto edge:edges_){
        edge.second->ComputeResidual();
        tempChi += edge.second->Chi2();    
    }
 
    //此处是计算近似使用dogleg步长更新理论上应该减小的损失
    double scale = 0;
    scale = delta_x_.transpose() * b_ ;
    std::cout<<"第一部分scale为 "<<scale<<endl;
    scale -= 0.5 * delta_x_.transpose() * Hessian_ * delta_x_; 
    scale += 1e-3;
    cout<<"scale = "<<scale<<endl;

    double rho = (currentChi_ - tempChi)/scale;
    std::cout << "rho: " << rho << " , chi= " << tempChi << " , delta= " << delta_
                  << std::endl;
    //迭代策略
    if(rho > 0 && isfinite(tempChi)){
        if(rho>0.75) delta_ = std::max(delta_, 3.*delta_x_.norm());
        else if(rho<0.25)   delta_ = delta_/2.;
        currentChi_ = tempChi;
        return true;    
    }
    else{
        delta_ = delta_/2.;
        return false;    
    }

}

实现

对于dogleg算法基于eigen实现了一般版本，下面是其应用于曲线拟合的实例。

参考文献

• [1] METHODS FOR NON-LINEAR LEAST SOUARES PROBLEMS. K.Madsen, H.B.Nielsen, O.Tingleff

• [2] Is Levenberg-Marquardt the Most Efficient Optimization Algorithm for Implementing Bundle Adjustment. Manolis I.A.