vins初始化中的尺度、重力、速度的初始化

最近这几天在看vins的源码，刚好前天写了初始化中如何确定陀螺仪的偏置，今天顺手将初始化中尺度、速度、重力向量的初始化也总结一下。

初始化

此处初始化的本质其实就是视觉sfm测量与imu预积分的松耦合对齐，也就是寻找最适合的待优化的变量使得sfm与imu预积分结果对的最齐。

首先，我们需要确定待初始化的变量有：

\[ \mathcal{X}_{I}^{3(n+1)+3+1}=\left[v_{b_{0}}^{b_{0}}, v_{b_{1}}^{b_{1}}, \ldots, v_{b_{n}}^{b_{n}}, g^{c_{0}}, s\right] \]

其中，\(v_{b_k}^{b_k}\)代表第k帧图像在其IMU坐标系下的速度，\(g^{c_0}\)代表第0帧相机坐标系下的重力向量，s是尺度。

如果熟练掌握了IMU预积分的知识，那么我们知道（其中是从k到k+1的预积分）：

\[ \begin{array}{c}{R_{w}^{b_{k}} p_{b_{k+1}}^{w}=R_{w}^{b_{k}}\left(p_{b_{k}}^{w}+v_{b_{k}}^{w} \Delta t_{k}-\frac{1}{2} g^{w} \Delta t_{k}^{2}\right)+\alpha_{b_{k+1}}^{b_{k}}} \\ {R_{w}^{b_{k}} v_{b_{k+1}}^{w}=R_{w}^{b_{k}}\left(v_{b_{k}}^{w}-g^{w} \Delta t_{k}\right)+\beta_{b_{k+1}}^{b_{k}}}\end{array} \]

在vio的初始化中，我们可以使用\(c_0\)代替\(w\)，并且将尺度\(s\)引入。得到下式：

\[ \begin{array}{c}{\alpha_{b_{k+1}}^{b_{k}}=R_{c_{0}}^{b_{k}}\left(s p_{b_{k+1}}^{c_{0}}-s p_{b_{k}}^{c_{0}}+\frac{1}{2} g^{c_{0}} \Delta t_{k}^{2}-R_{b_{k}}^{c_{0}} v_{b_{k}}^{b_{k}} \Delta t_{k}\right)} \\ {\beta_{b_{k+1}}^{b_{k}}=R_{c_{0}}^{b_{k}}\left(R_{b_{k+1}}^{c_{0}} v_{b_{k+1}}^{b_{k+1}}+g^{c_{0}} \Delta t_{k}-R_{b_{k}}^{c_{0}} v_{b_{k}}^{b_{k}}\right)}\end{array} \]

对于位置的预积分\(\alpha\)，将论文中式（14）带入，可以得到下式子：

\[ \begin{array}{c}{\delta \alpha_{b_{k+1}}^{b_{k}}=\alpha_{b_{k+1}}^{b_{k}}-R_{c_{0}}^{b_{k}}\left(s p_{b_{k+1}}^{c_{0}}-s p_{b_{k}}^{c_{0}}+\frac{1}{2} g^{c_{0}} \Delta t_{k}^{2}-R_{b_{k}}^{c_{0}} v_{b_{k}}^{b_{k}} \Delta t_{k}\right)} \\ {=\alpha_{b_{k+1}}^{b_{k}}-R_{c_{0}}^{b_{k}}\left(s p_{c_{k+1}}^{c_{0}}-R_{b_{k+1}}^{c_{0}} p_{c}^{b}-\left(s p_{c_{k}}^{c_{0}}-R_{b_{k}}^{c_{0}} p_{c}^{b}\right)+\frac{1}{2} g^{c_{0}} \Delta t_{k}^{2}-R_{b_{k}}^{c_{0}} v_{b_{k}}^{b_{k}} \Delta t_{k}\right)} \\ {=\alpha_{b_{k+1}}^{b_{k}}-R_{c_{0}}^{b_{k}} s\left(p_{c_{k+1}}^{c_{0}}-p_{c_{k}}^{c_{0}}\right)+R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} p_{c}^{b}-p_{c}^{b}+v_{b_{k}}^{b_{k}} \Delta t_{k}-\frac{1}{2} R_{c_{0}}^{b_{k}} g^{c_{0}} \Delta t_{k}^{2}=0_{3 \times 1}}\end{array} \]

上式中\(v_{b_k}^{b_k}\)、\(s\)、\(g^{c_0}\)是待优化变量，将其转换成\(Hx=b\)的形式（待优化变量都放到等式左边）：

\[ R_{c_{0}}^{b_{k}}\left(p_{c_{k+1}}^{c_{0}}-p_{c_{k}}^{c_{0}}\right) s-v_{b_{k}}^{b_{k}} \Delta t_{k}+\frac{1}{2} R_{c_{0}}^{b_{k}} \Delta t_{k}^{2} g^{c_{0}}= \alpha_{b_{k+1}}^{b_{k}}+R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} p_{c}^{b}-p_{c}^{b} \]

写成矩阵形式如下：

\[ \left[\begin{array}{cccc}{-I \Delta t_{k}} & {0} & {\frac{1}{2} R_{c_{0}}^{b_{k}} \Delta t_{k}^{2}} & {R_{c_{0}}^{b_{k}}\left(p_{c_{k+1}}^{c_{0}}-p_{c_{k}}^{c_{0}}\right)}\end{array}\right]\left[\begin{array}{c}{v_{b_{k}}^{b_{k}}} \\ {v_{b_{k+1}}^{b_{k+1}}} \\ {g^{c_{0}}} \\ {s}\end{array}\right]= \alpha_{b_{k+1}}^{b_{k}}+R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} p_{c}^{b}-p_{c}^{b} \]

同理，对于速度的预积分\(\beta\)，最后，可以得到下式（也就是论文中的公式18、19）:

\[ \left[\begin{array}{cccc}{-I \Delta t_{k}} & {0} & {\frac{1}{2} R_{c_{0}}^{b_{k}} \Delta t_{k}^{2}} & {R_{c_{0}}^{b_{k}}\left(p_{c_{k+1}}^{c_{0}}-p_{c_{k}}^{c_{0}}\right)} \\ {-I} & {R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}}} & {R_{c_{0}}^{b_{k}} \Delta t_{k}} & {0}\end{array}\right]\left[\begin{array}{c}{v_{b_{k}}^{b_{k}}} \\ {v_{b_{k+1}}^{b_{k+1}}} \\ {g^{c_{0}}} \\ {s}\end{array}\right] = \left[\begin{array}{c}{ \alpha_{b_{k+1}}^{b_{k}}+R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} p_{c}^{b}-p_{c}^{b}} \\ {\beta_{b_{k+1}}^{b_{k}}}\end{array}\right] \]

其中\(\beta\)与\(\alpha\)是预积分的测量值。

上式也就是\(H \mathcal{X}_{I} = b\)，这个公式我们将其等式两边同时乘以\(H^T\)，然后使用LDLT进行求解得到待优化的量。

vins中的代码实现

在vins中，作者是通过每两帧构建上面的一个约束，然后组合起来构建整个sfm范围内的约束，进行LDLT求解即可得到\(\mathcal{X}_{I}\)

代码实现在vins_estimator/src/initial/initial_aligment.cpp的LinearAlignment函数中。

重力细化

此处说是重力细化，其实是根据重力约束对整个初始化结果（包括尺度、速度等）进行细化。

上述方法得到的g一般是存在误差的。因为在实际应用中，当地的重力向量的模一般是已知固定大小的（所以只有两个自由度未知），而我们在前面求解时并没有利用这个条件，因此最后计算出来的重力向量很难刚好满足这个条件。于是，在vins的初始化中，还会对得到的重力向量进行修正。

首先，作者对重力向量进行参数化：

\[ \hat{g}=\|g\| \overline{\hat{g}}+w_{1} b_{1}+w_{2} b_{2}=\|g\| \overline{\hat{g}}+\vec{b}^{3 \times 2} w^{2 \times 1} \]

其中，\(\overline{\hat{g}}\)是上一步中估计得到的重力向量方向的单位向量，\(b_{1}\)与\(b_{2}\)是另外两个单位向量，是\(\overline{\hat{g}}\)切平面上的两个互相垂直的单位向量，获得方式如下：

gravity

gravity

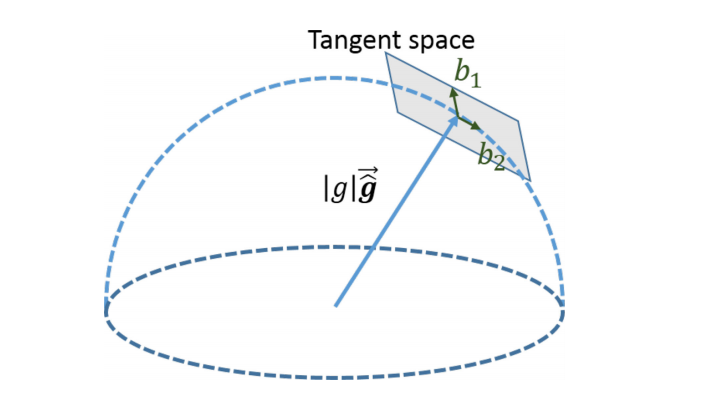
此时我们可以从上面的式子知道，原本三维的优化变量\(g^{c_{0}}\)已经可以使用两维的\(w^{2 \times 1}\)替代。参考上一节的推导，待优化变量变成了

\[ \left[\begin{array}{c}{v_{b_{k}}^{b_{k}}} \\ {v_{b_{k+1}}^{b_{k+1}}} \\ w^{2 \times 1} \\ {s}\end{array}\right] \]

最后得到的观测方程也变为了

\[ \left[\begin{array}{cccc}{-I \Delta t_{k}} & {0} & \frac{1}{2} R_{c_{0}}^{b_{k}} \Delta t_{k}^{2} \vec{b} & {R_{c_{0}}^{b_{k}}\left(p_{c_{k+1}}^{c_{0}}-p_{c_{k}}^{c_{0}}\right)} \\ {-I} & {R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}}} & {R_{c_{0}}^{b_{k}} \Delta t_{k} \vec{b}} & {0}\end{array}\right]\left[\begin{array}{c}{v_{b_{k}}^{b_{k}}} \\ {v_{b_{k+1}}^{b_{k+1}}} \\ w \\ {s}\end{array}\right] = \left[\begin{array}{c}{ \alpha_{b_{k+1}}^{b_{k}}+R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} p_{c}^{b}-p_{c}^{b}} - \frac{1}{2} R_{c_{0}}^{b_{c}} \Delta t_{k}^{2}\|g\| \overline{\hat{g}} \\ {\beta_{b_{k+1}}^{b_{k}} -R_{c_{0}}^{b_{k}} \Delta t_{k}\|g\| \hat{g}}\end{array}\right] \]

基于新得到的观测方程（可以使用LDLT分解求解），我们可以通过重力约束不断地对初始化结果进行修正，迭代对其进行求解（vins中迭代了4次），最后得到一个修正后的初始化结果。

vins中的代码实现

由于这个修正是基于原本的初始的重力向量进行的修正，因此原本的重力向量越准确，得到的效果也就越好，因此可以多迭代修正几次（vins中4次）

修正代码实现在vins_estimator/src/initial/initial_aligment.cpp的RefineGravity函数中。

与世界坐标系对齐

这一步一般是最后一步，一般世界坐标系选择的是东北天坐标系。则这个对齐操作就是得到将重力向量旋转到Z轴上的旋转矩阵，这个旋转矩阵就是将原本坐标变换到世界坐标系（东北天坐标系）的变换矩阵。

找到这个变换矩阵后，接下来就是使用这个变换矩阵将位姿，速度等状态信息都变换到世界坐标系下。

加速度计bias

通过上面的阅读，我们会发现在vins的初始化中并没有对加速度计的bias进行估计，感觉对于超定的方程，多计算一个加速度计的bias好像也不是什么难事，，而且建模应该会更准确。在这个初始化工作的论文中其实有解释原因：

1. 通过仿真实验证明，如果运动不剧烈，加速度计的bias很难被观测出来；

2. 忽略加速计的bias对估计其他初始值的影响不大；

3. 加速度计的bias是可以通过之后的VIO紧耦合优化，慢慢估计出来的；

4. 在VI-orb中有对加速度计的bias进行估计，其收敛需要好几秒，并且没有一个好的判定条件来判断加速度计bias的估计是否正确。

其实此处介绍的初始化方法并不是第一版vins中的方法，现在的初始化方法是参考VI-orb中的初始化方式改进而来的。下面的三篇论文是它们在相互借鉴的基础上产生的

1. 第一版vins的初始化论文：Monocular Visual-Inertial State Estimation with Online Initialization and Camera-IMU Extrinsic Calibration (2017, HKUST)

2. VI-orb的初始化论文：Visual-Inertial Monocular SLAM With Map Reuse (2017 VI-ORB)

3. 当前vins初始化工作的论文：Robust Initialization of Monocular Visual-Inertial Estimation on Aerial Robots (2017, HKUST)

参考资料

• [1] https://github.com/HKUST-Aerial-Robotics/VINS-Mono
• [2] VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator, Tong Qin, Peiliang Li, Zhenfei Yang, Shaojie Shen, IEEE Transactions on Robotics