slam中的滑动窗口法
随着VSLAM系统不断往新环境探索,就会有新的相机姿态以及看到新的环境特征,最小二乘残差就会越来越多,信息矩阵越来越大,计算量也会越来越大。
为了保持优化变量的个数在一定范围内,需要使用滑动窗口算法动态增加或移除优化变量。
滑动窗口算法
流程
增加新的变量进入最小二乘系统优化
如果变量数目达到了一定的维度,则移除老的变量
系统不断循环前面两步
信息矩阵
一般对于基于高斯分布的最大似然估计转化的最小二乘问题,对应的高斯牛顿求解为:
\[ \underbrace{\mathbf{J}^{\top} \boldsymbol{\Sigma}^{-1} \mathbf{J}}_{\mathbf{H} \text { or } \Lambda} \delta \boldsymbol{\xi}=\underbrace{-\mathbf{J}^{\top} \boldsymbol{\Sigma}^{-1} \mathbf{r}}_{\mathbf{b}} \]
其中\(\Sigma\)对应的是测量的协方差矩阵(它的逆是测量的信息矩阵),而\(H\)是优化变量的信息矩阵。
此处的信息矩阵H其实是当前观测残差r引入系统的不确定度矩阵,也可以理解为当前观测带给系统状态变量的信息矩阵。而不是系统本来存在的先验信息矩阵。
利用边际概率移除老的变量(Marginalization)
直接丢弃变量和对应的测量值,会损失信息。正确的做法是使用边际概率,将丢弃变量所携带的信息传递给剩余变量。
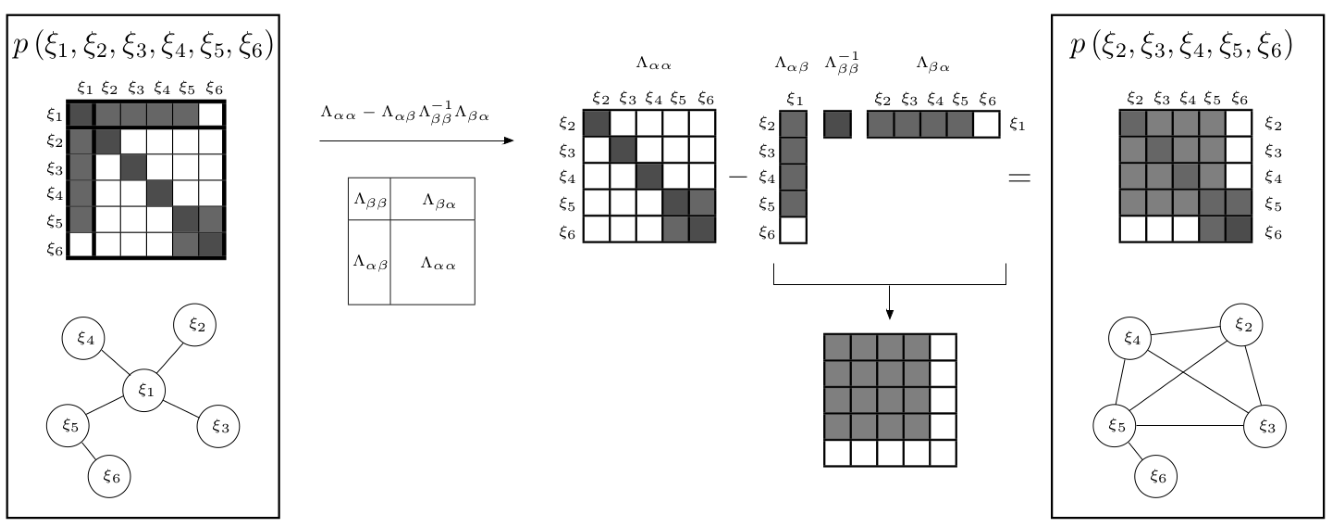
下面,本文使用一个例子A来演示一下,下面这个例子中,我们使用边界概率移除变量\(\xi_{1}\)。信息矩阵的变化过程如下:
接下来,再通过一个例子B,这个例子中,我们先加入一个\(x_{t+1}\)变量,然后再移除\(x_{t}\)变量,整个变化过程如下:
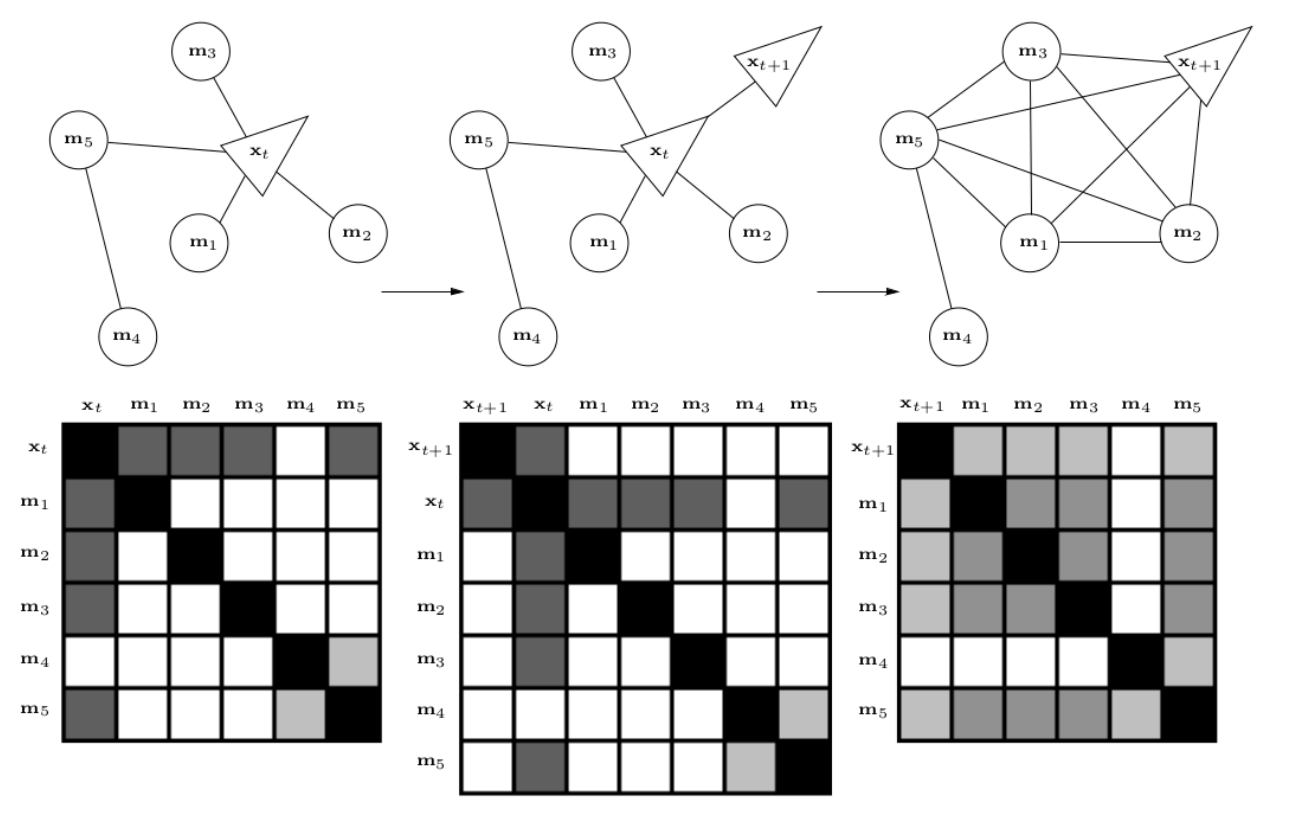
我们可以发现,marginalization会使得信息矩阵变稠密,原先条件独立的变量,可能变得相关。这个原因是因为信息矩阵中会包含间接相关性。
移除旧变量,添加新变量
这里还是使用这个例子,完整过程如下:

此例中,其实对于这么一个高斯牛顿问题:
\[ \underbrace{\mathbf{J}^{\top} \boldsymbol{\Sigma}^{-1} \mathbf{J}}_{\mathbf{H} \text { or } \Lambda} \delta \boldsymbol{\xi}=\underbrace{-\mathbf{J}^{\top} \boldsymbol{\Sigma}^{-1} \mathbf{r}}_{\mathbf{b}} \]
在marg之前,被marg的变量\(x_m\)以及对应的测量\(\mathcal{S}_{m}\),它们构建的那部分最小二乘信息矩阵为:(k表示k时刻): \[ \begin{aligned} \mathbf{b}_{m}(k) &=\left[\begin{array}{c}{\mathbf{b}_{m m}(k)} \\ {\mathbf{b}_{m r}(k)}\end{array}\right]=-\sum_{(i, j) \in \mathcal{S}_{m}} \mathbf{J}_{i j}^{\top}(k) \mathbf{\Sigma}_{i j}^{-1} \mathbf{r}_{i j} \\ \boldsymbol{\Lambda}_{m}(k) &=\left[\begin{array}{cc}{\boldsymbol{\Lambda}_{m m}(k)} & {\boldsymbol{\Lambda}_{m r}(k)} \\ {\boldsymbol{\Lambda}_{r m}(k)} & {\boldsymbol{\Lambda}_{r r}(k)}\end{array}\right]=\sum_{(i, j) \in \mathcal{S}_{m}} \mathbf{J}_{i j}^{\top}(k) \boldsymbol{\Sigma}_{i j}^{-1} \mathbf{J}_{i j}(k) \end{aligned} \]
此处原本的等式关系为 \[ \left[\begin{array}{cc}{\boldsymbol{\Lambda}_{m m}(k)} & {\boldsymbol{\Lambda}_{m r}(k)} \\ {\boldsymbol{\Lambda}_{r m}(k)} & {\boldsymbol{\Lambda}_{r r}(k)}\end{array}\right] \left[\begin{array}{c}{\delta x_{m}} \\ { \delta x_{r}}\end{array}\right] = \left[\begin{array}{c}{\mathbf{b}_{m m}(k)} \\ {\mathbf{b}_{m r}(k)}\end{array}\right] \] 此处我们希望marg掉\(x_m\)部分,只保留\(x_r\),因此直接使用舒尔补进行消元:
\[ \left[\begin{array}{cc}{I} & 0 \\ -{\boldsymbol{\Lambda}_{r m}(k)} {\boldsymbol{\Lambda}_{m m}^{-1}(k)} & I \end{array}\right] \left[\begin{array}{cc}{\boldsymbol{\Lambda}_{m m}(k)} & {\boldsymbol{\Lambda}_{m r}(k)} \\ {\boldsymbol{\Lambda}_{r m}(k)} & {\boldsymbol{\Lambda}_{r r}(k)}\end{array}\right] \left[\begin{array}{c}{\delta x_{m}} \\ { \delta x_{r}}\end{array}\right] = \left[\begin{array}{cc}{I} & 0 \\ -{\boldsymbol{\Lambda}_{r m}(k)} {\boldsymbol{\Lambda}_{m m}^{-1}(k)} & I \end{array}\right] \left[\begin{array}{c}{\mathbf{b}_{m m}(k)} \\ {\mathbf{b}_{m r}(k)}\end{array}\right] \] 得到: \[ \left[\begin{array}{cc}{\boldsymbol{\Lambda}_{m m}(k)} & {\boldsymbol{\Lambda}_{m r}(k)} \\ 0 & {\boldsymbol{\Lambda}_{r r}(k)-\boldsymbol{\Lambda}_{r m}(k) \boldsymbol{\Lambda}_{m m}^{-1}(k) \boldsymbol{\Lambda}_{m r}(k)} \end{array}\right] \left[\begin{array}{c}{\delta x_{m}} \\ { \delta x_{r}}\end{array}\right] = \left[\begin{array}{c}{\mathbf{b}_{m m}(k)} \\ {\mathbf{b}_{m r}(k) - {\boldsymbol{\Lambda}_{r m}(k)} {\boldsymbol{\Lambda}_{m m}^{-1}(k)} \mathbf{b}_{m m}(k)} \end{array}\right] \]
marg之后(只保留下面一行),变量\(x_{m}\)的测量信息是这样传递给剩下的变量\(x_{r}\)的:
\[ \begin{array}{l}{\mathbf{b}_{p}(k)=\mathbf{b}_{m r}(k)-\boldsymbol{\Lambda}_{r m}(k) \boldsymbol{\Lambda}_{m m}^{-1}(k) \mathbf{b}_{m m}(k)} \\ {\boldsymbol{\Lambda}_{p}(k)=\boldsymbol{\Lambda}_{r r}(k)-\boldsymbol{\Lambda}_{r m}(k) \boldsymbol{\Lambda}_{m m}^{-1}(k) \boldsymbol{\Lambda}_{m r}(k)}\end{array} \]
其中下标\(p\)表示prior,即这些信息将构建一个关于\(x_{r}\)的先验信息。
此处的信息矩阵其实与状态的先验协方差关系不大似乎,因此不是传统意义上的信息矩阵。此处信息矩阵倒是可以理解为本次观测引入的不确定度矩阵(本次观测引入的信息矩阵),而滑窗中的marg操作,就是在marg掉一部分变量时,不断的将之前对该部分变量的观测引入系统的不确定度继续保留在系统中,使得系统滑窗过程中的信息损失不至于太大。
在\(k^{\prime}\)时刻,新残差\(r_{27}\)和先验信息\(b_{p}(k),\Lambda_{p}(k)\)以及残差\(r_{56}\)构建新的最小二乘问题:
\[ \begin{array}{c}{\mathbf{b}\left(k^{\prime}\right)=\mathbf{\Pi}^{\top} \mathbf{b}_{p}(k)-\sum_{(i, j) \in \mathcal{S}_{a}\left(k^{\prime}\right)} \mathbf{J}_{i j}^{\top}\left(k^{\prime}\right) \mathbf{\Sigma}_{i j}^{-1} \mathbf{r}_{i j}\left(k^{\prime}\right)} \\ {\mathbf{\Lambda}\left(k^{\prime}\right)=\mathbf{\Pi}^{\top} \mathbf{\Lambda}_{p}(k) \mathbf{\Pi}+\sum_{(i, j) \in \mathcal{S}_{a}\left(k^{\prime}\right)} \mathbf{J}_{i j}^{\top}\left(k^{\prime}\right) \mathbf{\Sigma}_{i j}^{-1} \mathbf{J}_{i j}\left(k^{\prime}\right)}\end{array} \]
\[\mathbf{\Pi}=\left[\begin{array}{ll}{\mathbf{I}_{\operatorname{dim} \mathbf{x}_{r}}} & {\mathbf{0}}\end{array}\right]\]
其中\(\mathbf{\Pi}\)用来将矩阵的维度进行扩张。\(S_{a}\)用来表示除被marg掉的测量以外的其他测量,如\(r_{56},r_{27}\)。
此处和被marg掉的变量相关的边(测量)也被丢弃了,所以先验信息中它们关于剩下的变量\(x_{r}\)的雅克比在后续求解中不能更新。而保留下来的边关于剩下的变量\(x_{r}\)的雅克比在后续求解中是不断更新的(在最新的线性化点处计算)
First Estimate Jacobians
就在上面这个例子中
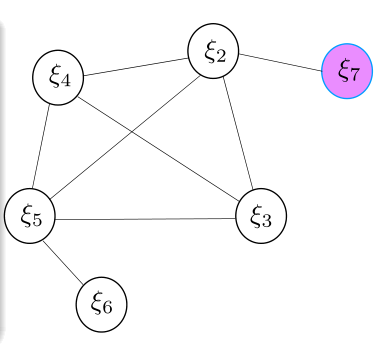
它在添加新的节点中信息矩阵的更新过程如下:
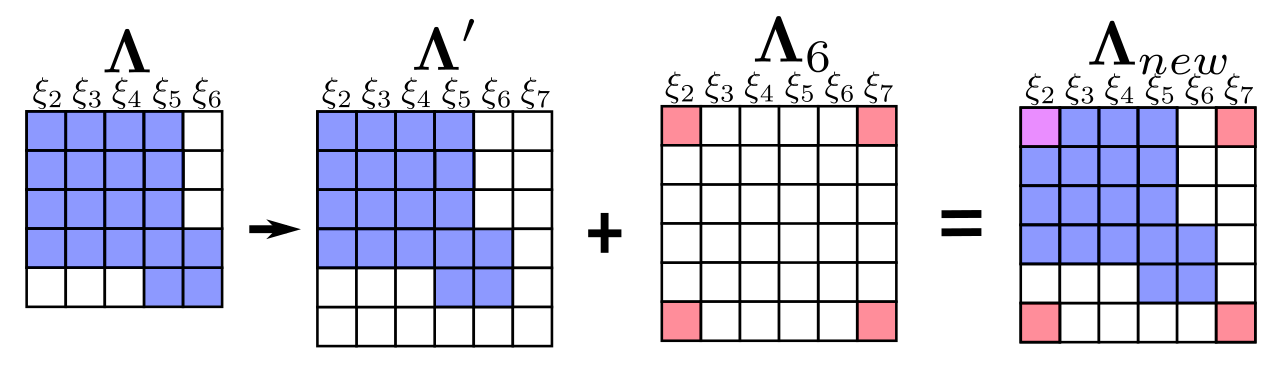
此时,我们会发现\(\xi_{2}\)自身的信息矩阵部分是由两部分组成的,此时如果这两部分的计算时使用的\(\xi_{2}\)(线性化点)的状态不一样,就可能会导致信息矩阵的零空间发生变化,引入错误信息。
之所以线性化点会不一样,是因为在marg掉\(\xi_{1}\)时,新得到的蓝色的小一维雅克比矩阵是直接通过舒尔补计算得到的,所以此时当时计算这个雅克比的\(\xi_{2}\)点的状态是迭代更新前的,此时新加入的粉红部分的雅克比要想保持与其一致,其在对\(\xi_{2}\)进行偏导计算时,也需要使用迭代更新前的状态才行。
此时FEJ的做法是:不同残差对同一个状态求雅克比时,线性化点必须一致。这样就能避免零空间退化而使得不客观变量变得可观。
参考文献
- [1] 深蓝学院vio课程讲义
- [2] Walter M R, Eustice R M, Leonard J J. Exactly Sparse Extended Information Filters for Feature-based SLAM[J]. Int.j.robotics Res, 2007, 26(4):335-359.
- [3] Dong-Si T C , Mourikis A I . Consistency analysis for sliding-window visual odometry[J]. Proceedings - IEEE International Conference on Robotics and Automation, 2012:5202-5209.