舒尔补与marginalization
在slam中经常会使用滑动窗口法来控制非线性优化的计算量级,此时当从现有的窗口中去除旧的变量时,如何调整信息矩阵就成为了一个棘手的问题。这篇博客就是要介绍如何使用舒尔补来简单的完成这个任务。
舒尔补
给定任意的矩阵块M,如下所示:
\[ \mathbf{M}=\left[\begin{array}{ll}{\mathbf{A}} & {\mathbf{B}} \\ {\mathbf{C}} & {\mathbf{D}}\end{array}\right] \]
- 如果,矩阵块D是可逆的,则\(\mathbf{A}-\mathbf{B D}^{-1} \mathbf{C}\)称之为D关于M的舒尔补。
- 如果,矩阵块A是可逆的,则\(\mathbf{D}-\mathbf{C A}^{-1} \mathbf{B}\)称之为A关于M的舒尔补。
舒尔补的来由
当我们想要将矩阵M变成上三角或者下三角过程中,都会遇到舒尔补,如下:
\[ \left[\begin{array}{cc}{\mathbf{I}} & {\mathbf{0}} \\ {-\mathbf{C A}^{-1}} & {\mathbf{I}}\end{array}\right]\left[\begin{array}{ll}{\mathbf{A}} & {\mathbf{B}} \\ {\mathbf{C}} & {\mathbf{D}}\end{array}\right]=\left[\begin{array}{cc}{\mathbf{A}} & {\mathbf{B}} \\ {\mathbf{0}} & {\Delta_{\mathbf{A}}}\end{array}\right] \]
\[ \left[\begin{array}{cc}{\mathbf{A}} & {\mathbf{B}} \\ {\mathbf{C}} & {\mathbf{D}}\end{array}\right]\left[\begin{array}{cc}{\mathbf{I}} & {-\mathbf{A}^{-1} \mathbf{B}} \\ {\mathbf{0}} & {\mathbf{I}}\end{array}\right]=\left[\begin{array}{cc}{\mathbf{A}} & {0} \\ {\mathbf{C}} & {\Delta_{\mathbf{A}}}\end{array}\right] \]
其中,不论是上三角还是下三角,都是\(\Delta_{\mathrm{A}}=\mathbf{D}-\mathbf{C A}^{-1} \mathbf{B}\)。联合起来,可以将M便形成对角形:
\[ \left[\begin{array}{cc}{\mathbf{I}} & {\mathbf{0}} \\ {-\mathbf{C A}^{-1}} & {\mathbf{I}}\end{array}\right]\left[\begin{array}{ll}{\mathbf{A}} & {\mathbf{B}} \\ {\mathbf{C}} & {\mathbf{D}}\end{array}\right]\left[\begin{array}{rr}{\mathbf{I}} & {-\mathbf{A}^{-1} \mathbf{B}} \\ {\mathbf{0}} & {\mathbf{I}}\end{array}\right]=\left[\begin{array}{cc}{\mathbf{A}} & {\mathbf{0}} \\ {\mathbf{0}} & {\Delta_{\mathbf{A}}}\end{array}\right] \]
反过来,我们又能从对角形恢复成矩阵M:
\[ \left[\begin{array}{cc}{\mathbf{I}} & {\mathbf{0}} \\ {\mathbf{C A}^{-1}} & {\mathbf{I}}\end{array}\right]\left[\begin{array}{cc}{\mathbf{A}} & {\mathbf{0}} \\ {\mathbf{0}} & {\Delta_{\mathbf{A}}}\end{array}\right]\left[\begin{array}{cc}{\mathbf{I}} & {\mathbf{A}^{-1} \mathbf{B}} \\ {\mathbf{0}} & {\mathbf{I}}\end{array}\right]=\left[\begin{array}{cc}{\mathbf{A}} & {\mathbf{B}} \\ {\mathbf{C}} & {\mathbf{D}}\end{array}\right] \]
此处注意有这么个性质:
\[ \left[\begin{array}{cc}{\mathbf{I}} & {-\mathbf{A}^{-1} \mathbf{B}} \\ {\mathbf{0}} & {\mathbf{I}}\end{array}\right]\left[\begin{array}{cc}{\mathbf{I}} & {\mathbf{A}^{-1} \mathbf{B}} \\ {\mathbf{0}} & {\mathbf{I}}\end{array}\right]=\mathbf{I} \]
所以还可以这样计算M的的逆:
\[ \left[\begin{array}{cc}{\mathbf{A}} & {\mathbf{B}} \\ {\mathbf{C}} & {\mathbf{D}}\end{array}\right]^{-1}=\left[\begin{array}{cc}{\mathbf{I}} & {-\mathbf{A}^{-1} \mathbf{B}} \\ {\mathbf{0}} & {\mathbf{I}}\end{array}\right]\left[\begin{array}{cc}{\mathbf{A}^{-1}} & {\mathbf{0}} \\ {\mathbf{0}} & {\Delta_{\mathbf{A}}^{-1}}\end{array}\right]\left[\begin{array}{cc}{\mathbf{I}} & {\mathbf{0}} \\ {-\mathbf{C A}^{-1}} & {\mathbf{I}}\end{array}\right] \]
将舒尔补应用于多元高斯分布
假设多元变量\(x\)服从高斯分布,且由两部分组成:\(\mathbf{x}=\left[\begin{array}{l}{a} \\ {b}\end{array}\right]\),变量之间构成的协方差矩阵为:
\[ \mathbf{K}=\left[\begin{array}{cc}{A} & {C^{\top}} \\ {C} & {D}\end{array}\right] \]
其中\(A=\operatorname{cov}(a, a), D=\operatorname{cov}(b, b), C=\operatorname{cov}(a, b)\)。由此变量\(x\)的概率分布为:
\[ P(a, b)=P(a) P(b | a) \propto \exp \left(-\frac{1}{2}\left[\begin{array}{l}{a} \\ {b}\end{array}\right]^{\top}\left[\begin{array}{cc}{A} & {C^{\top}} \\ {C} & {D}\end{array}\right]^{-1}\left[\begin{array}{l}{a} \\ {b}\end{array}\right]\right) \]
利用上面介绍的舒尔补的性质,我们可以对高斯分布进行分解,得到如下:
\[ \begin{array}{l}{P(a, b)} \\ {\propto \exp \left(-\frac{1}{2}\left[\begin{array}{l}{a} \\ {b}\end{array}\right]^{\top}\left[\begin{array}{cc}{A} & {C^{\top}} \\ {C} & {D}\end{array}\right]^{-1}\left[\begin{array}{l}{a} \\ {b}\end{array}\right]\right)} \\ {\propto \exp \left(-\frac{1}{2}\left[\begin{array}{c}{a} \\ {b}\end{array}\right]^{\top}\left[\begin{array}{cc}{I} & {-A^{-1} C^{\top}} \\ {0} & {I}\end{array}\right]\left[\begin{array}{cc}{A^{-1}} & {0} \\ {0} & {\Delta_{\mathrm{A}}^{-1}}\end{array}\right]\left[\begin{array}{cc}{I} & {0} \\ {-C A^{-1}} & {I}\end{array}\right]\left[\begin{array}{c}{a} \\ {b}\end{array}\right]\right)} \\ {\propto \exp \left(-\frac{1}{2}\left[a^{\top} \quad\left(b-C A^{-1} a\right)^{\top}\right]\left[\begin{array}{cc}{A^{-1}} & {0} \\ {0} & {\Delta_{\mathrm{A}}^{-1}}\end{array}\right]\left[\begin{array}{c}{a} \\ {b-C A^{-1} a}\end{array}\right]\right)} \\ {\propto \exp \left(-\frac{1}{2}\left(a^{\top} A^{-1} a\right)+\left(b-C A^{-1} a\right)^{\top} \Delta_{\mathrm{A}}^{-1}\left(b-C A^{-1} a\right)\right)} \\ {\propto \underbrace{\exp \left(-\frac{1}{2} a^{\top} A^{-1} a\right)}_{p(a)} \underbrace{\exp \left(-\frac{1}{2}\left(b-C A^{-1} a\right)^{\top} \Delta_{\mathrm{A}}^{-1}\left(b-C A^{-1} a\right)\right)}_{p(b | a)}} \end{array} \]
这意味着我们能从多元高斯分布\(P(a,b)\)中分解得到边界概率\(p(a)\)和条件概率p(b|a)
原先分布的协方差矩阵与信息矩阵
我们已知的协方差矩阵的逆就是信息矩阵,它们是如下的关系:
\[ \left[\begin{array}{cc}{A} & {C^{\top}} \\ {C} & {D}\end{array}\right]^{-1}=\left[\begin{array}{cc}{A^{-1}+A^{-1} C^{\top} \Delta_{\mathrm{A}}^{-1} C A^{-1}} & {-A^{-1} C^{\top} \Delta_{\mathrm{A}}^{-1}} \\ {-\Delta_{\mathrm{A}}^{-1} C A^{-1}} & {\Delta_{\mathrm{A}}^{-1}}\end{array}\right] \triangleq\left[\begin{array}{cc}{\Lambda_{a a}} & {\Lambda_{a b}} \\ {\Lambda_{b a}} & {\Lambda_{b b}}\end{array}\right] \]
分离出来的边界概率分布
分离出来的边界概率分布就是\(p(a)\),它是在滑动窗口法中使用的方法,它是marg掉b之后剩下的分布。
分离出来的边界概率分布的信息矩阵是(可以发现协方差矩阵不变,信息矩阵刚好变为移除变量信息矩阵的舒尔补):
\[ \begin{array}{l}{P(a)=\int_{b} P(a, b)} \\ {P(a) \propto \exp \left(-\frac{1}{2} a^{\top} A^{-1} a\right) \sim \mathcal{N}(0, A)}\end{array} \]
分离出来的边界概率分布的信息矩阵是:
\[ A^{-1}=\Lambda_{a a}-\Lambda_{a b} \Lambda_{b b}^{-1} \Lambda_{b a} \]
此处我们会发现,分离出来的边界分布变量之间的协方差是不变的,但是信息矩阵改变了。这是因为信息矩阵中的相关计算是遵循链式法则,在分离出来的变量固定住以后,原本不想关的变量可以变成相关的。
分离出来的条件概率分布
分离出来a后的条件概率分布的协方差矩阵变为a对应的舒尔补,均值也变了。
\[ P(b | a) \propto \exp \left(-\frac{1}{2}\left(b-C A^{-1} a\right)^{\top} \Delta_{\mathrm{A}}^{-1}\left(b-C A^{-1} a\right)\right) \]
分离出来的条件概率分布的信息矩阵是:
\[ \Delta_{A}^{-1}=\Lambda_{b b} \]
总结
其实我们在marg掉变量的时候,我们需要搞清楚自己想要获得的是边界概率还是条件概率。在滑动窗口中是保留边界概率。从联合分布得到边际概率
从上面的分析我们可以发现,边界概率对于协方差矩阵的操作是很容易的,但是不好操作信息矩阵。条件概率分布相反,对于信息矩阵容易操作,但是不好操作协方差矩阵。
对于原分布:
\[ P(\boldsymbol{a}, \boldsymbol{b})=\mathcal{N}\left(\left[\begin{array}{c}{\boldsymbol{\mu}_{a}} \\ {\boldsymbol{\mu}_{b}}\end{array}\right],\left[\begin{array}{cc}{\boldsymbol{\Sigma}_{a a}} & {\boldsymbol{\Sigma}_{a b}} \\ {\boldsymbol{\Sigma}_{b a}} & {\boldsymbol{\Sigma}_{b b}}\end{array}\right]\right)=\mathcal{N}^{-1}\left(\left[\begin{array}{c}{\boldsymbol{\eta}_{a}} \\ {\boldsymbol{\eta}_{b}}\end{array}\right],\left[\begin{array}{cc}{\boldsymbol{\Lambda}_{a a}} & {\mathbf{\Lambda}_{a a}} \\ {\boldsymbol{\Lambda}_{b a}} & {\boldsymbol{\Lambda}_{b b}}\end{array}\right]\right) \]
两种marg变量的方式后剩下的可以用表格总结如下(其中在slam中一般比较多的使用信息矩阵的边际概率marg时的公式
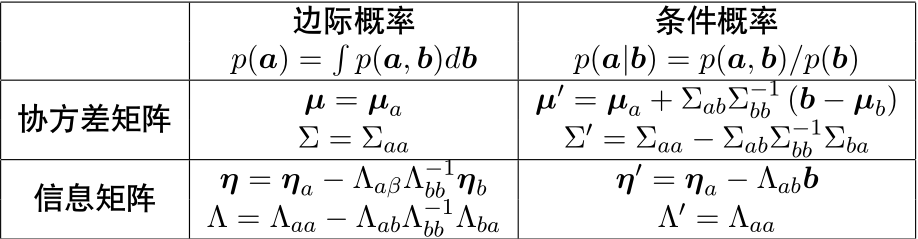
schur补的操作在slam中十分常见,其实在前面BA的博客已经提到过一次了,这次系统的、概念性的介绍一下。它的主要作用是消元简化计算。在ba的介绍中中侧重加速解方程,此处介绍侧重加速求解边界概率。
参考文献
- [1] 深蓝学院vio课程讲义
- [2] Huang. Conditional and marginal distributions of a multivariate Gaussian.