多元高斯分布的协方差矩阵与信息矩阵

零均值的多元高斯分布有如下概率形式：

\[ p(\mathbf{x}) - \frac{1}{Z} \exp \left(-\frac{1}{2} \mathbf{x}^{\top} \mathbf{\Sigma}^{-1} \mathbf{x}\right) \]

其中\(\mathbf{\Sigma}\)是协方差矩阵，协方差矩阵的逆可以记作\(\mathbf{\Lambda}=\mathbf{\Sigma}^{-1}\)，也叫信息矩阵。当变量\(\mathbf{x}\)是三维变量时，协方差矩阵为：

\[ \boldsymbol{\Sigma} = \left[\begin{array}{ccc}{\Sigma_{11}} & {\Sigma_{12}} & {\Sigma_{13}} \\ {\Sigma_{21}} & {\Sigma_{22}} & {\Sigma_{23}} \\ {\Sigma_{31}} & {\Sigma_{32}} & {\Sigma_{33}} \end{array}\right] \]

其中\(\Sigma_{i j} = E\left(x_{i} x_{j}\right)\)

其实在应用中，往往我们直接操作的是信息矩阵，而不是协方差矩阵。下面从一个例子来体会一下协方差矩阵与信息矩阵。

example

假设\(x_{2}\)为室外的温度，\(x_{1},x_{3}\)分别是房间1与房间3的室内温度：

\[ \begin{aligned} x_{2} &= v_{2} \\ x_{1} &= w_{1} x_{2} + v_{1} \\ x_{3} &= w_{3} x_{2}+v_{3} \end{aligned} \]

其中，\(v_{i}\)为相互独立，且各自服从协方差为\(\sigma_{i}^{2}\)的高斯分布。根据上面它们之间的联系，我们可以求出\(x\)的协方差矩阵，首先：

\[ \begin{aligned} \Sigma_{11}=E\left(x_{1} x_{1}\right) &=E\left(\left(w_{1} v_{2}+v_{1}\right)\left(w_{1} v_{2}+v_{1}\right)\right) \\ &=w_{1}^{2} E\left(v_{2}^{2}\right)+2 w_{1} E\left(v_{1} v_{2}\right)+E\left(v_{1}^{2}\right) \\ &=w_{1}^{2} \sigma_{2}^{2}+\sigma_{1}^{2} \end{aligned} \]

然后同理，可以求出另外两个对角元素为\(\Sigma_{22}=\sigma_{2}^{2}, \Sigma_{33}=w_{3}^{2} \sigma_{2}^{2}+\sigma_{3}^{2}\)。而对于协方差矩阵的非对角元素有：

\[ \begin{array}{l}{\Sigma_{12}=E\left(x_{1} x_{2}\right)=E\left(\left(w_{1} v_{2}+v_{1}\right) v_{2}\right)=w_{1} \sigma_{2}^{2}} \\ {\Sigma_{13}=E\left(\left(w_{1} v_{2}+v_{1}\right)\left(w_{3} v_{2}+v_{3}\right)\right)=w_{1} w_{3} \sigma_{2}^{2}}\end{array} \]

依次类似，可以得到完整的协方差矩阵为：

\[ \boldsymbol{\Sigma}=\left[\begin{array}{ccc}{w_{1}^{2} \sigma_{2}^{2}+\sigma_{1}^{2}} & {w_{1} \sigma_{2}^{2}} & {w_{1} w_{3} \sigma_{2}^{2}} \\ {w_{1} \sigma_{2}^{2}} & {\sigma_{2}^{2}} & {w_{3} \sigma_{2}^{2}} \\ {w_{1} w_{3} \sigma_{2}^{2}} & {w_{3} \sigma_{2}^{2}} & {w_{3}^{2} \sigma_{2}^{2}+\sigma_{3}^{2}}\end{array}\right] \]

信息矩阵是协方差矩阵的逆矩阵，此处我们可以通过计算联合高斯分布来得到协方差矩阵的逆：

\[ \begin{aligned} p\left(x_{1}, x_{2}, x_{3}\right) &=p\left(x_{2}\right) p\left(x_{1} | x_{2}\right) p\left(x_{3} | x_{2}\right) \\ &=\frac{1}{Z_{2}} \exp \left(-\frac{x_{2}^{2}}{2 \sigma_{2}^{2}}\right) \frac{1}{Z_{1}} \exp \left(-\frac{\left(x_{1}-w_{1} x_{2}\right)^{2}}{2 \sigma_{1}^{2}}\right) \frac{1}{Z_{3}} \exp \left(-\frac{\left(x_{3}-w_{3} x_{2}\right)^{2}}{2 \sigma_{3}^{2}}\right) \end{aligned} \]

利用指数性质，可以计算出联合概率分布如下：

\[ \begin{array}{l}{p\left(x_{1}, x_{2}, x_{3}\right)} \\ {\quad=\frac{1}{Z} \exp \left(-\frac{x_{2}^{2}}{2 \sigma_{2}^{2}}-\frac{\left(x_{1}-w_{1} x_{2}\right)^{2}}{2 \sigma_{1}^{2}}-\frac{\left(x_{3}-w_{3} x_{2}\right)^{2}}{2 \sigma_{3}^{2}}\right)} \\ {\quad=\frac{1}{Z} \exp \left(-x_{2}^{2}\left[\frac{1}{2 \sigma_{2}^{2}}+\frac{w_{1}^{2}}{2 \sigma_{1}^{2}}-\frac{w_{3}^{2}}{2 \sigma_{3}^{2}}\right]-x_{1}^{2} \frac{1}{2 \sigma_{1}^{2}}+2 x_{1} x_{2} \frac{w_{1}}{2 \sigma_{1}^{2}}-x_{3}^{2} \frac{1}{2 \sigma_{3}^{2}}+2 x_{3} x_{2} \frac{w_{3}}{2 \sigma_{3}^{2}}\right)} \\ {\quad=\frac{1}{Z} \exp \left(-\frac{1}{2}\left[\begin{array}{ccc}{x_{1}} & {x_{2}} & {x_{3}}\end{array}\right]\left[\begin{array}{cccc}{\frac{1}{\sigma_{1}^{2}}} & {-\frac{w_{1}}{\sigma_{1}^{2}}} & {0} \\ {-\frac{w_{1}}{\sigma_{1}^{2}}} & {\frac{w_{1}^{2}}{\sigma_{1}^{2}}+\frac{1}{\sigma_{2}^{2}}+\frac{w_{3}^{2}}{\sigma_{1}^{2}}} & {-\frac{w_{3}}{\sigma_{3}^{2}}} \\ {0} & {-\frac{w_{3}}{\sigma_{3}^{2}}} & {\frac{1}{\sigma_{3}^{2}}}\end{array}\right]\left[\begin{array}{c}{x_{1}} \\ {x_{2}} \\ {x_{3}}\end{array}\right]\right)}\end{array} \]

所以，这里上面矩阵就是协方差矩阵的逆，也就是信息矩阵：

\[ \boldsymbol{\Lambda}=\mathbf{\Sigma}^{-1}=\left[\begin{array}{ccc}{\frac{1}{\sigma_{1}^{2}}} & {-\frac{w_{1}}{\sigma_{1}^{2}}} & {0} \\ {-\frac{w_{1}}{\sigma_{1}^{2}}} & {\frac{w_{1}^{2}}{\sigma_{1}^{2}}+\frac{1}{\sigma_{1}^{2}}+\frac{w_{3}^{2}}{\sigma_{1}^{2}}} & {-\frac{w_{3}}{\sigma_{3}^{2}}} \\ {0} & {-\frac{w_{3}^{2}}{\sigma_{3}^{2}}} & {\frac{1}{\sigma_{3}^{2}}}\end{array}\right] \]

由上，可以看到当在协方差矩阵中，\(x_{1}\)与\(x_{3}\)之间是相关的，而在信息矩阵中，它们是相互独立的（相关系数为0）,这是因为，我们在推导信息矩阵时是使用了联合分布的链式法则，信息矩阵中\(x_{1}\)与\(x_{3}\)的相关性在\(x_{2}\)确定之后计算的，此时它们是相互独立的。

上述例子中去掉\(x_{3}\)

协方差矩阵直接只计算前两个相关的协方差矩阵即可，也就是去掉划线的部分

变为：

marg

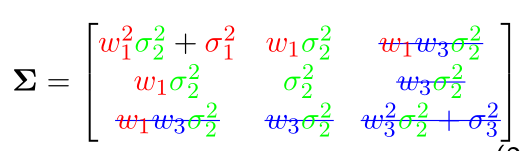
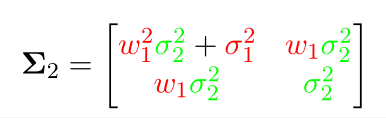
至于信息矩阵，只需要把信息矩阵公式中\(x_{3}\)相关的部分（蓝色）去掉：

得到：

marg

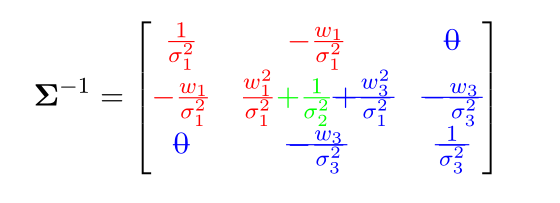
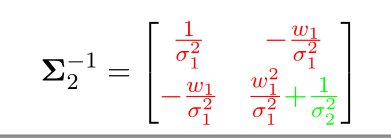
之所以要移除一个变量，然后再算它的信息矩阵，是因为在实际应用中经常会用到这样的操作，上面只讲了原理，下面会抽时间讲讲如何快速实现，会需要舒尔补(Schur's complement)与边缘化(marginalization)。

补充

此处需要注意，协方差矩阵与信息矩阵都可以用来表示多元变量之间的相关性。但是，协方差矩阵是衡量的变量之间边界概率关系，通常是直接相关性，信息矩阵会有间接相关性，衡量的是变量之间的条件概率关系。因此，在计算中我们会发现有些协方差矩阵中相关的两个量在信息矩阵中不相关，有些协方差矩阵中不相关的两个量在信息矩阵中相关。

比如在下面这个例子中

\[ x_{2}=w_{1} x_{1}+w_{3} x_{3}+v_{2} \]

marg

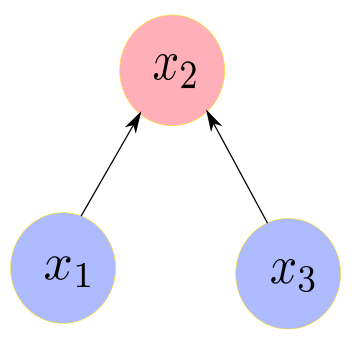
协方差矩阵为：

\[ \boldsymbol{\Sigma}=\left[\begin{array}{cccc}{\sigma_{1}^{2}} & {w_{1} \sigma_{1}^{2}} & {0} \\ {w_{1} \sigma_{1}^{2}} & {\sigma_{2}^{2}+w_{1}^{2} \sigma_{1}^{2}+w_{3}^{2} \sigma_{3}^{2}} & {w_{3} \sigma_{3}^{2}} \\ {0} & {w_{3} \sigma_{3}^{2}} & {\sigma_{3}^{2}}\end{array}\right] \]

信息矩阵为：

\[ \left[\begin{array}{ccc}{\frac{1}{\sigma_{1}^{2}}+\frac{w_{1}^{2}}{\sigma_{2}^{2}}} & {-\frac{w_{1}}{\sigma_{2}^{2}}} & {\frac{w_{1} w_{3}}{\sigma_{2}^{2}}} \\ {-\frac{w_{1}}{\sigma_{2}^{2}}} & {\frac{1}{\sigma_{2}^{2}}} & {-\frac{w_{3}}{\sigma_{2}^{2}}} \\ {\frac{w_{1} w_{3}}{\sigma_{2}^{2}}} & {-\frac{w_{3}}{\sigma_{2}^{2}}} & {\frac{1}{\sigma_{3}^{2}}+\frac{w_{3}^{2}}{\sigma_{2}^{2}}}\end{array}\right] \]

\(x_{1}\)与\(x_{3}\)在协方差矩阵中不相关，在信息矩阵中相关。这是因为协方差矩阵中是直接相关性，信息矩阵可以使用链式法则推导，其中当\(x_2\)固定后，这两个变量就会变成相关的了。

参考文献

• [1] 深蓝学院vio课程讲义
• [2] David Mackay. "The humble Gaussian distribution". In:(2006).