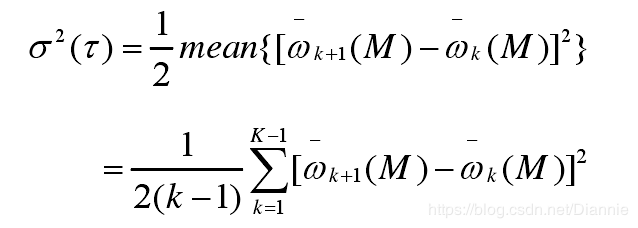imu的数学模型与误差标定问题
IMU数学模型
加速度计
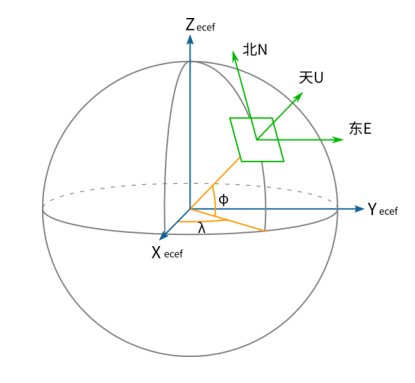
首先,对于世界坐标系,一般我们会使用最常见的东北天(ENU)坐标系G(无关远点位置,只与姿态有关)。在这个坐标系中,重力加速度为
\[g^G = (0,0,-9.81)^T\]。
此时,假设IMU坐标系就是ENU坐标系,则\(R_{IB}=I\),静止时有(其中\(a_{m}\)是测量值):
\[a = 0\]
\[a_{m} = -g\]
所以,不静止时:(此处对a和g符号不做区分标记,因为假设body系与Global系一样)
\[a_{m} = a - g \]
由上可知,其实在物体做自由落体时imu测量的加速度才是0,静止时反而是\(-g\),这个是由加速度计的测量原理决定的。
上面讲的是在IMU坐标系也是ENU坐标系时的情况(此时位置无关,只关乎姿态)。大多数实际应用中,IMU坐标系(Body)一般是与ENU坐标系有一个姿态的变化的。此时,得到的理论测量值为:
\[ a_{m}^{B} = R_{BG} (a^{G} - g^{G}) \]
此处\(R_{BG}\)是将Global坐标转换到Body坐标姿态的旋转矩阵。此处可以看出,global坐标系的位置与body坐标系的位置与在两个系下测量的加速度大小无关。但是,与姿态有关。
陀螺仪
相比较于加速度计,陀螺仪相对简单。如果不考虑误差,则
\[ w_{m}^{B} = w^{B} \]
我们会发现此处并没有向加速度计一样,将global坐标系下的角速度转换到陀螺仪的测量值,而是直接使用body系下的角速度。这是因为旋转叠加时(比如四元数和旋转矩阵表示姿态时),全局姿态是直接乘以body系下的更新量的就可以得到新的全局姿态的。
恢复运动轨迹
imu最后输出的是一个离散的加速度、角速度序列。我们想做的是利用这些恢复出运动的轨迹(也就是一个位姿的序列)。
下面会介绍两种离散积分的方法。欧拉法与中值法。
这两种方法,都是已知了\(k\)时刻的位姿,\(k\)时刻与\(k+1\)时刻的测量值(加速度与角速度)。目的是求得\(k+1\)时刻的位姿。
欧拉法
欧拉法,是直接使用\(k\)时刻的测量值\(a,w\)来积分。
\[ \mathbf{p}_{w b_{k+1}}=\mathbf{p}_{w b_{k}}+\mathbf{v}_{k}^{w} \Delta t+\frac{1}{2} \mathbf{a} \Delta t^{2} \]
\[ \mathbf{v}_{k+1}^{w}=\mathbf{v}_{k}^{w}+\mathbf{a} \Delta t \]
\[ \mathbf{q}_{w b_{k+1}}=\mathbf{q}_{w b_{k}} \otimes\left[\begin{array}{c}{1} \\ {\frac{1}{2} \omega \delta t}\end{array}\right] \]
其中
\[ \mathbf{a} = \mathbf{q}_{w b_{k}} \mathbf{a}^{b_{k}} - \mathbf{g}^{w} \]
\[ \boldsymbol{\omega} = \boldsymbol{\omega}^{b_{k}} \]
中值法
中值法,使用两个相邻时刻\(k\)到\(k+1\)的位姿是用两个时刻的测量值\(a,w\)的平均值来离散积分。
\[ \mathbf{p}_{w b_{k+1}}=\mathbf{p}_{w b_{k}}+\mathbf{v}_{k}^{w} \Delta t+\frac{1}{2} \mathbf{a} \Delta t^{2} \]
\[ \mathbf{v}_{k+1}^{w}=\mathbf{v}_{k}^{w}+\mathbf{a} \Delta t \]
\[ \mathbf{q}_{w b_{k+1}}=\mathbf{q}_{w b_{k}} \otimes\left[\begin{array}{c}{1} \\ {\frac{1}{2} \omega \delta t}\end{array}\right] \]
其中
\[ \mathbf{a} = \frac{1}{2} \left(\mathbf{q}_{w b_{k}} \mathbf{a}^{b_{k}} + \mathbf{q}_{w b_{k+1}} \mathbf{a}^{b_{k+1}} \right) - \mathbf{g}^{w} \]
\[ \boldsymbol{\omega} = \frac{1}{2} \left(\boldsymbol{\omega}^{b_{k}} + \boldsymbol{\omega}^{b_{k+1}} \right) \]
代码
1 | |
此处推荐一个生成imu数据、加噪声与测试的工具,这里中值积分与欧拉积分可以参考上面的我的代码,因为工具里可能不一定提供了。
旋转积分
上面恢复姿态轨迹的积分用了四元数的形式,下面我想多介绍几个
此处\(w\)是imu的测量结果,也就是局部角速度。因为这个旋转积分的结果是姿态,因此下面会分别介绍使用四元数、SO3还有欧拉角下的积分方式。
- 四元数的形式:
\[ \mathbf{q}_{w b^{\prime}}=\mathbf{q}_{w b} \otimes\left[\begin{array}{c}{1} \\ {\frac{1}{2} \boldsymbol{\omega} \Delta t}\end{array}\right] \]
- \(SO3\)形式:
\[ \mathbf{R}_{w b^{\prime}}=\mathbf{R}_{w b} \exp (\boldsymbol{\omega} \cdot \Delta t) \]
- 欧拉角形式:
\[ \vartheta w b^{\prime}=\vartheta_{w b}+E_{w b} \cdot \omega \Delta t \]
我们可以发现,这三种方法,对于全局姿态的变化,旋转矩阵与四元数都是直接使用imu的测量(也就是局部角速度)进行更新的。只有在欧拉角的形式里,\(E_{w b}\)表示将IMU body坐标系下的角速度转化成欧拉角速度。此处可以推导出\(E_{w b}\),这个是三种方法中唯一一个需要转换的地方。原因的话,我觉得这是因为累加与累乘的区别,欧拉角不支持乘法。如果使用角度来表示旋转矩阵与四元数,此时对角度的更新也得使用加法(原来角度加上角速度与时间的积即为新的角度),但是四元数与旋转矩阵本身是只支持乘法的,它们是直接乘以局部扰动即可。
欧拉角速度到imu输出角速度
这个挺有必要的,因为用欧拉角来表示姿态还是很方便的。
step1:绕着惯性坐标系的z轴旋转,得到新的坐标系\(b^{1}\)
step2:绕着新坐标系\(b^{1}\)的y轴旋转得到坐标系\(b^{2}\)
step3:绕着新坐标系\(b^{2}\)的x轴旋转得到坐标系\(b^{3}\),\(b^{3}\)就是我们的body坐标系
欧拉角速度到body角速度:
\[ \begin{aligned} \boldsymbol{\omega} &=R(\psi) R(\theta)\left\{\begin{array}{c}{0} \\ {0} \\ {\frac{d \phi}{d t}}\end{array}\right\}+R(\psi)\left\{\begin{array}{c}{0} \\ {\frac{d \theta}{d t}} \\ {0}\end{array}\right\}+\left\{\begin{array}{c}{\frac{d \psi}{d t}} \\ {0} \\ {0}\end{array}\right\} \\ &=\left[\begin{array}{ccc}{1} & {0} & {-\sin \theta} \\ {0} & {\cos \psi} & {\sin \psi \cos \theta} \\ {0} & {-\sin \psi} & {\cos \psi \cos \theta}\end{array}\right]\left\{\begin{array}{l}{\frac{d \psi}{d t}} \\ {\frac{d \psi}{d t}} \\ {\frac{d \phi}{d t}}\end{array}\right\} \end{aligned} \]
上面取逆就得到,如下body到欧拉角的变换:
\[ \frac{d \boldsymbol{\vartheta}}{d t}=\left[\begin{array}{ccc}{1} & {\sin \psi \tan \theta} & {\cos \psi \tan \theta} \\ {0} & {\cos \psi} & {-\sin \psi} \\ {0} & {\sin \psi / \cos \theta} & {\cos \psi / \cos \theta}\end{array}\right] \vec{\omega} \]
误差与标定
加速度计和陀螺仪的误差可以分为确定性误差与随机误差。
确定性误差
确定性误差可以事先标定确定,包括:bias,scale ...
bias
理论上,当没有外部作用时,IMU传感器的输出应该为0。但是,实际上数据存在一个偏置b。
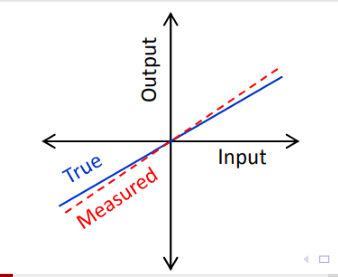
scale
scale可以看成是实际数值和传感器输出值之间的比值。
Nonorthogonality/Misalignment Errors
在多轴IMU传感器制作的时候,由于制作工艺的问题的问题,会使得\(xyz\)轴可能不垂直,这个也叫轴间误差。
轴间误差使得本来x轴的分量会对测量到的y轴与z轴的分量有影响。将其与scale误差相结合,会得到如下的测量与实际的对应关系。
\[\left[\begin{array}{l}{a_{m x}} \\ {a_{m y}} \\ {a_{m z}}\end{array}\right]=\left[\begin{array}{lll}{s_{x x}} & {m_{x y}} & {m_{x z}} \\ {m_{y x}} & {s_{y y}} & {m_{y z}} \\ {m_{z x}} & {m_{z y}} & {s_{z z}}\end{array}\right]\left[\begin{array}{l}{a_{x}} \\ {a_{y}} \\ {a_{z}}\end{array}\right]\]
其他确定性误差
bias与scale的误差是会受温度影响的,并且在运行中也许也会改变。
确定新误差的标定(六面法)
以加速度计为例,陀螺仪同理
指将加速度计的3个轴分别朝上或者朝下水平放置一段时间(对于陀螺仪就是在三个旋转轴上正反旋转,不过需要高精度转台),采集六个面的数据完成标定。
3个轴都是正交时
\[ bias = \frac{l_{f}^{up} + l_{f}^{down}}{2} \]
\[ scale = \frac{l_{f}^{up} - l_{f}^{down}}{2*g} \]
其中,\(l\)为加速度计某个轴的测量值,\(g\)为当地的重力加速度。
当具有轴间误差时
此时实际加速度和测量值之间的关系为:
\[ \left[\begin{array}{l}{l_{a x}} \\ {l_{a y}} \\ {l_{a z}}\end{array}\right]=\left[\begin{array}{lll}{s_{x x}} & {m_{x y}} & {m_{x z}} \\ {m_{y x}} & {s_{y y}} & {m_{y z}} \\ {m_{z x}} & {m_{z y}} & {s_{z z}}\end{array}\right]\left[\begin{array}{l}{a_{x}} \\ {a_{y}} \\ {a_{z}}\end{array}\right]+\left[\begin{array}{l}{b_{a x}} \\ {b_{a y}} \\ {b_{a z}}\end{array}\right] \]
水平静止放置6面的时候,加速度的理论值为:
\[ a_{1}=\left[\begin{array}{l}{g} \\ {0} \\ {0}\end{array}\right], a_{2}=\left[\begin{array}{c}{-g} \\ {0} \\ {0}\end{array}\right], a_{3}=\left[\begin{array}{l}{0} \\ {g} \\ {0}\end{array}\right], a_{4}=\left[\begin{array}{c}{0} \\ {-g} \\ {0}\end{array}\right], a_{5}=\left[\begin{array}{l}{0} \\ {0} \\ {g}\end{array}\right], a_{6}=\left[\begin{array}{c}{0} \\ {0} \\ {-g}\end{array}\right] \]
对应的测量值矩阵L:
\[ \mathbf{L}=\left[\begin{array}{llllll}{\mathbf{l}_{1}} & {\mathbf{l}_{2}} & {\mathbf{l}_{3}} & {\mathbf{l}_{4}} & {\mathbf{l}_{5}} & {\mathbf{l}_{6}}\end{array}\right] \]
利用最小二乘就能够把12个变量求出来。
随机误差
随机误差主要有两部分,一个是高斯白噪声,一个是bias随机游走。
高斯白噪声
IMU数据连续时间上受到一个均值为0,方差为\(\sigma\),各时刻之间相互独立的高斯过程\(n(t)\):
\[ \begin{array}{l}{E[n(t)] \equiv 0} \\ {E\left[n\left(t_{1}\right) n\left(t_{2}\right)\right]=\sigma^{2} \delta\left(t_{1}-t_{2}\right)}\end{array} \]
其中\(\delta()\)表示狄拉克函数。
不过需要说明的是,实际上,IMU传感器获取的数据为离散采样,离散和连续高斯白噪声的方差之间存在如下转换关系:
\[ \begin{aligned} n_{d}[k] & \triangleq n\left(t_{0}+\Delta t\right) \simeq \frac{1}{\Delta t} \int_{t_{0}}^{t_{0}+\Delta t} n(\tau) d t \\ E\left(n_{d}[k]^{2}\right) &=E\left(\frac{1}{\Delta t^{2}} \int_{t_{0}}^{t_{0}+\Delta t} \int_{t_{0}}^{t_{0}+\Delta t} n(\tau) n(t) d \tau d t\right) \\ &=E\left(\frac{\sigma^{2}}{\Delta t^{2}} \int_{t_{0}}^{t_{0}+\Delta t} \int_{t_{0}}^{t_{0}+\Delta t} \delta(t-\tau) d \tau d t\right) \\ &=E\left(\frac{\sigma^{2}}{\Delta t}\right) \end{aligned} \]
即离散的序列的方差是连续的方差除以\(\Delta t\)(传感器的采样时间),也就是乘以采样频率f。(下面\(\sigma\)是标准差,一般参数文件里写的也是标准差)
\[ \sigma_{d} = \sigma \frac{1}{\sqrt{\Delta t}} \]
bias
随机游走
通常使用维纳过程来建模bias随时间连续变化的过程,离散时间下称之为随机游走。
\[ \dot{b}(t)=n(t)=\sigma_{b} w(t) \]
bias的变化的导数是其中\(w\)是方差为1的白噪声。
同样,离散和连续之间的转换为:
\[ \begin{aligned} b_{d}[k] \triangleq & b\left(t_{0}\right)+\int_{t_{0}}^{t_{0}+\Delta t} n(t) d t \\ E\left(\left(b_{d}[k]-b_{d}[k-1]\right)^{2}\right) &=E\left(\int_{t_{0}+\Delta t}^{t_{0}+\Delta t} \int_{t_{0}}^{t_{0}+\Delta t} n(t) n(\tau) d \tau d t\right) \\ &=E\left(\sigma_{b}^{2} \int_{t_{0}}^{t_{0}+\Delta t} \int_{t_{0}}^{t_{0}+\Delta t} \delta(t-\tau) d \tau d t\right) \\ &=E\left(\sigma_{b}^{2} \Delta t\right) \end{aligned} \]
bias随机游走离散序列的噪声方差是连续的方差乘以\(\Delta t\)倍(传感器的采样时间),也就是除以采样频率f。
\[ \sigma_{bd}=\sigma_{b}\sqrt{\Delta t} \]
随机误差的标定(艾伦方差标定)
Allan方差法是20世纪60年代由美国国家标准局的David Allan提出的,它是一种基于时域的分析方法。具体流程如下:
保持传感器绝对静止获取数据
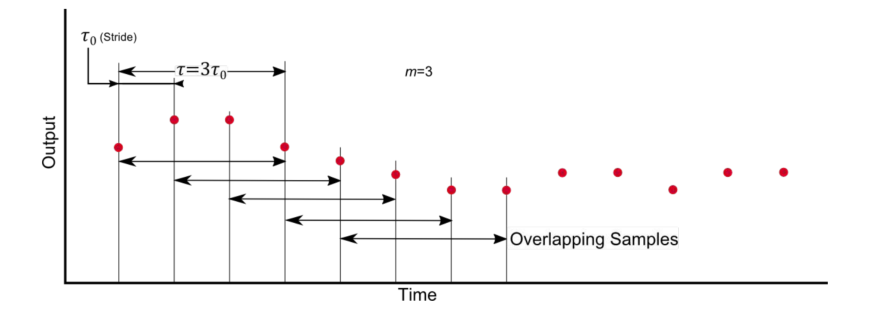
对数据进行分段,设置时间段的时长,如下图所示。
将传感器数据按照时间段进行平均。
计算方差,绘制艾伦曲线。
- 此处的艾伦方差的计算公式如下(将每个时间段长度作为一个变量,将每个时间段的数据求均值,计算方差):
- 忽略其他噪声的影响,Allan方差可以近似为各种噪声的和,化简为:
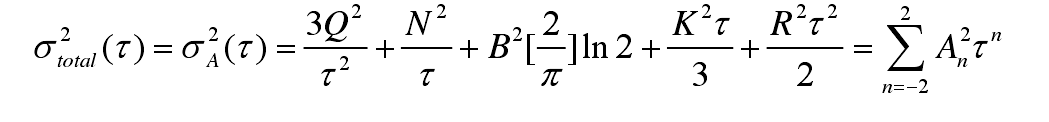
其中,Q:量化噪声误差系数;N:角速度随机游走误差系数;B:零偏不稳定性误差系数;K:速率随机游走误差系数;R:速率斜坡误差系数

(ps:其中表格中B那一项是乘法不是除法,写错了)
这里,绘制出来的艾伦曲线如下图所示:
其中t=1,斜率为-0.5处纵坐标的值为高斯白噪声方差,斜率为0.5,t=3处的纵坐标的值为随机游走方差。
下面给出两个github上的比较好用的标定工具。
imu_utils,额注意,这个工具的结果关于bias那一项输出的是bias稳定性的方差,不是随机游走的方差,因此,我们需要此工具生成的艾伦方差曲线自行完成bias随机游走方差的获得。。
加上误差模型后的理论测量值
- 加速度计
\[ \mathbf{a}_{m}^{B}=\mathbf{S}_{a} \mathbf{R}_{B G}\left(\mathbf{a}^{G}-\mathbf{g}^{G}\right)+\mathbf{n}_{a}+\mathbf{b}_{a} \]
- 陀螺仪
\[ \boldsymbol{\omega}_{m}^{B}=\mathbf{S}_{g} \boldsymbol{\omega}^{B}+\mathbf{n}_{g}+\mathbf{b}_{g} \]
- 低端传感器,可能会出现加速度影响陀螺仪的值的情况,也就是下面的第二项:
\[ \boldsymbol{\omega}_{m}^{B}=\mathbf{S}_{g} \boldsymbol{\omega}^{B}+\mathbf{s}_{g a} \mathbf{a}^{B}+\mathbf{n}_{g}+\mathbf{b}_{g} \]
参考资料
- [1] 深蓝学院vio课程
- [2] https://blog.csdn.net/Diannie/article/details/88062687