三维中间中旋转的表示方式--欧拉角、旋转矩阵、旋转向量、四元数
三维空间中的旋转有很多种表示方式,欧拉角,旋转矩阵,旋转向量,四元数。由于在slam与机器人中会大量用到这方面的知识,所以在这里将此方面的知识总结一下,方便以后查阅。
在slam系统中一般使用四元数来存储姿态(也有使用旋转矩阵的,不过比较少),不使用旋转向量,个人认为原因主要在于:
- 首先得到一个旋转向量之后,我们是不可以直接通过类似相加的方式对旋转向量进行更新的,而矩阵和四元数的更新(乘法)是有现成的运算定义的。
- 四元数相比较旋转矩阵,只需要4个参数;并且在求得姿态增量(一个旋转向量)时,转成对应四元数的计算更简单,旋转矩阵需要罗德里格斯公式要麻烦一点;四元数乘法比矩阵乘法更快;
- 不过通过旋转矩阵(李群)的表示精度会更高一点,四元数形式需要的计算量和内存会小一点(不过现在感觉对这些也不是很敏感了)。
欧拉角(Euler Angle)
欧拉角可以使用滑翔翼飞行器控制来理解,比如对于下面这张图,一般假设红色轴为z轴,则z轴表示空间的第三维,则去掉这一维度表示飞行器在一个二维平面上;蓝色轴为x轴,也是飞行器的朝向,因此绕此轴转动就像是飞行器在做翻滚动作,因此叫翻滚角(roll);绿色轴为y轴,绕这个轴转动其实就是飞机开始准备向上飞或者向下飞了,因此叫俯仰角(pitch);同理,绕红色轴也就是z轴转动代表飞机开始调整自身在二维平面上的朝向了,因此叫偏航角(yaw)。
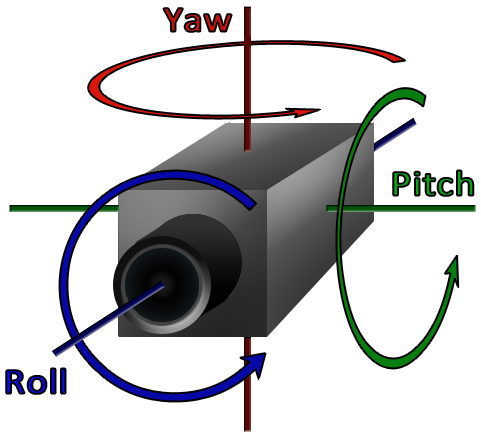
在欧拉角的表示中,yaw、pitch、roll的顺序对旋转结果是有影响的。即给定一组欧拉角角度值,比如yaw=45度,pitch=30度,roll=60度,按照yaw-pitch-roll的顺序旋转和按照yaw-roll-pitch的顺序旋转,最终刚体的朝向是不同的!换言之,若刚体需要按照两种不同的旋转顺序旋转到相同的朝向,所需要的欧拉角角度值则是不同的!
另外需要注意的是,在欧拉角的表示方式里,三个旋转轴一般是随着刚体在运动,即wikipedia中所谓的intrinsic rotation,见下图动画所示(图来自wikipedia)。相对应的另一种表示方式是,三个旋转轴是固定的,不随刚体旋转而旋转,即extrinsic rotation,这种表示方式在计算机视觉中不是很常用。
欧拉角的优点是非常直观,但是会有以下几个缺点:
- 欧拉角表示方式不唯一。由上面分析知道当yaw、pitch、roll的顺序变换后,会有不同的组合可以达到同样的效果。
- 万向锁问题。
万向锁问题:因为飞行器的朝向即为x轴的方向,所以欧拉角三个轴是一直在变的。比如在yaw-pitch-roll这种顺序的欧拉角姿态调整中,在中间pitch俯仰角度调整为90度时,当前的x轴会与初始的z轴重合,即接下来进行roll的角度调整时其实与第一次yaw角度调整是在同一个轴(初始的z轴)上进行的,这使得系统平白丢失了一个自由度(进行了三次旋转,但是其实两次旋转就可以完成)。
旋转矩阵
其实在计算坐标变换时,我们使用最多的表示旋转的方式是其实旋转矩阵。三维空间中的旋转矩阵是3×3的矩阵,将欧拉角变换为旋转矩阵的计算方式如下:
\[ \begin{array}{rlr}{R(\alpha, \beta, \gamma)} & {=R_{z}(\alpha) R_{y}(\beta) R_{x}(\gamma)=} \\ {} & {\left(\begin{array}{cc}{\cos \alpha \cos \beta} & {\cos \alpha \sin \beta \sin \gamma-\sin \alpha \cos \gamma} & {\cos \alpha \sin \beta \cos \gamma+\sin \alpha \sin \gamma} \\ {\sin \alpha \cos \beta} & {\sin \alpha \sin \beta \sin \gamma+\cos \alpha \cos \gamma} & {\sin \alpha \sin \beta \cos \gamma-\cos \alpha \sin \gamma} \\ {-\sin \beta} & {\cos \beta \sin \gamma} & {\cos \beta \cos \gamma}\end{array}\right)}\end{array} \]
\[ R_{z}(\alpha)=\left(\begin{array}{ccc}{\cos \alpha} & {-\sin \alpha} & {0} \\ {\sin \alpha} & {\cos \alpha} & {0} \\ {0} & {0} & {1}\end{array}\right) \]
\[ R_{y}(\beta)=\left(\begin{array}{ccc}{\cos \beta} & {0} & {\sin \beta} \\ {0} & {1} & {0} \\ {-\sin \beta} & {0} & {\cos \beta}\end{array}\right) \]
\[ R_{x}(\gamma)=\left(\begin{array}{ccc}{1} & {0} & {0} \\ {0} & {\cos \gamma} & {-\sin \gamma} \\ {0} & {\sin \gamma} & {\cos \gamma}\end{array}\right) \]
其中,\(\alpha\)、\(\beta\)、\(\gamma\)分别是欧拉角的yaw、pitch和roll角。上述结果是三个旋转矩阵(三个角度上的旋转)连续相乘的结果。
由上,我们可以看出,如果yaw、pitch和roll的顺序发生改变,矩阵相乘的顺序需要作出相应改变,所得的旋转矩阵的结果也会发生变化。
此外,其实旋转矩阵也叫作方向余弦矩阵(Direction Cosine Matrix),简称DCM,这种表示叫法在陀螺力学领域较为常用。DCM的名字来历其实是用欧拉角之外的另一种用三个角度值表示三维旋转的方式。这种表示方法原理是:假设刚体在起始朝向时三个坐标轴的向量为\(I,J,K\),而刚体在目标朝向时的三个坐标轴的向量为\(i,j,k\),则该旋转可以通过三个坐标轴分别与原始坐标轴的夹角表示,如下图所示:旋转矩阵虽然有9个元素,但是其实只有三个自由度,所以旋转矩阵各行各列之间一定是互相正交的,同时因为旋转矩阵的不包含尺度变换,因此旋转矩阵一定要是正交矩阵(逆矩阵等于转置矩阵)
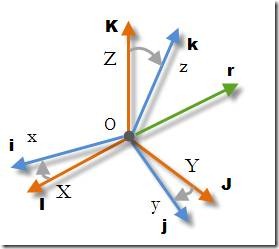
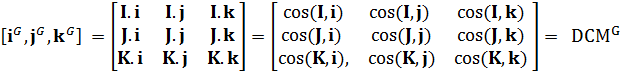
DCM就是旋转矩阵。
旋转向量
旋转向量是使用三维向量的形式来表示旋转。三维空间中的任意一个旋转,都是可以用绕三维空间中的某个轴旋转过某个角度(轴角表示)来表示,这就是所谓的\(Axis-Angle\)表示方法。这种表示方法中,轴\(Axis\)可以使用一个三维单位向量\((x,y,z)\)来表示,\(Angle\)可以使用一个角度值\(\theta\)来表示。所以,客观来说,一个四维向量\((\theta, x, y, z)\)就可以表示出三维空间任意的旋转。但是其实可以使用更紧凑的表示方式--旋转向量\((\theta \ast x, \theta \ast y, \theta \ast z)\)来表示三维空间中的任意旋转。
旋转向量\((\theta \ast x, \theta \ast y, \theta \ast z)\)的来源是轴角表示。它与旋转矩阵的转换可以通过指数映射与罗德里格斯公式完成。
四元数
旋转矩阵的表示具有冗余性(使用9个量表示3个自由度的旋转),欧拉角和旋转向量是紧凑的,但是具有奇异性。所以,此处我们会再介绍一种常用的表示旋转的方式,四元数(Quaternion)。
四元数使用复数的形式来表示旋转
\[ \boldsymbol{q}=q_{0}+q_{1} i+q_{2} j+q_{3} k \]
其中\(i,j,k\)是四元数的三个虚部。这三个虚部满足关系式:
\[ \left\{\begin{array}{l}{i^{2}=j^{2}=k^{2}=-1} \\ {i j=k, j i=-k} \\ {j k=i, k j=-i} \\ {k i=j, i k=-j}\end{array}\right. \]
所以,也可以使用一个标量与一个向量来表示四元数:
\[ \boldsymbol{q}=[s, \boldsymbol{v}], \quad s=q_{0} \in \mathbb{R}, \boldsymbol{v}=\left[q_{1}, q_{2}, q_{3}\right]^{T} \in \mathbb{R}^{3} \]
同时,我们一般使用单位四元数来表示三维空间中任意一个旋转。对于绕单位向量\(\boldsymbol{n}=\left[n_{x}, n_{y}, n_{z}\right]^{T}\)进行了角度为\(\theta\)的旋转,这个旋转的四元数形式为:
\[ \boldsymbol{q}=\left[\cos \frac{\theta}{2}, n_{x} \sin \frac{\theta}{2}, n_{y} \sin \frac{\theta}{2}, n_{z} \sin \frac{\theta}{2}\right]^{T} \]
此处需要说明的是,对于旋转的角度\(\theta\),我们将其加上\(2 \pi\),得到的四元数\(q\)会变为\(-q\),所以,四元数有一个性质,任意旋转可以使用两个互为相反数的四元数来表示。并且从上面这个公式,我们也可以看出,使用单位四元数可以表示任意一个旋转。
并且,对于一个旋转角度为0的旋转,表示它的四元数是:
\[ \boldsymbol{q}_{0}=[ \pm 1,0,0,0]^{T} \]
反之,从四元数中恢复出轴角可以使用如下:
\[ \left\{\begin{array}{l}{\theta=2 \arccos q_{0}} \\ {\left[n_{x}, n_{y}, n_{z}\right]^{T}=\left[q_{1}, q_{2}, q_{3}\right]^{T} / \sin \frac{\theta}{2}}\end{array}\right. \]
之所以四元数会这么受欢迎(虽然它很不直观),是因为它有一些神奇的性质。
四元数的神奇1
第一个,我们使用四元数对一个三维点\(\boldsymbol{p}=[x, y, z] \in \mathbb{R}^{3}\)进行旋转变换(旋转由一个轴角\(\boldsymbol{n}, \theta\)指定)。此时,首先将三维空间点用一个虚四元数来描述:
\[ \boldsymbol{p}=[0, x, y, z]=[0, \boldsymbol{v}] \]
这相当于我们把四元数的三个虚部与空间中的三个轴相对应。然后用四元数\(q\)来表示这个旋转:
\[ \boldsymbol{q}=\left[\cos \frac{\theta}{2}, \boldsymbol{n} \sin \frac{\theta}{2}\right] \]
那么旋转后的点\(p^{\prime}\)可以表示为如下的乘积:
\[ \boldsymbol{p}^{\prime}=\boldsymbol{q} \boldsymbol{p} \boldsymbol{q}^{-1} \]
最后的计算结果的实部一定为0,所以是纯虚四元数表示一个空间点位置。
四元数的神奇2(乘法)
首先四元数的复数形式是:
\[ \boldsymbol{q}=q_{0}+q_{1} i+q_{2} j+q_{3} k \]
对于两个四元数
\[\mathbf{q}_{1}=\left(\begin{array}{llll}{a_{1}} & {b_{1}} & {c_{1}} & {d_{1}}\end{array}\right)^{T} \]
\[\mathbf{q}_{2}=\left(\begin{array}{llll}{a_{2}} & {b_{2}} & {c_{2}} & {d_{2}}\end{array}\right)^{T}\]
他们的乘积为(不可交换)就是两个复数想成的结果:
\[ \mathbf{q}_{1} \mathbf{q}_{2}=\left(\begin{array}{c}{a_{1} a_{2}-b_{1} b_{2}-c_{1} c_{2}-d_{1} d_{2}} \\ {a_{1} b_{2}+b_{1} a_{2}+c_{1} d_{2}-d_{1} c_{2}} \\ {a_{1} c_{2}-b_{1} d_{2}+c_{1} a_{2}+d_{1} b_{2}} \\ {a_{1} d_{2}+b_{1} c_{2}-c_{1} b_{2}+d_{1} a_{2}}\end{array}\right) \]
之所以介绍,四元数的乘法,是因为,对于两次旋转的叠加,是可以直接使用四元数的乘法实现。
并且,从上面的乘法,我们也可以看出,对于四元数来说,对应单位矩阵的四元数是(1,0,0,0),同时四元数的逆其实就等于四元数的共轭。
四元数相对时间的导数
首先,先介绍一个四元数关于轴角的表示(上面也有讲过):
\[ \boldsymbol{q}=\left[\cos \frac{\theta}{2}, \boldsymbol{n} \sin \frac{\theta}{2}\right] \]
所以这样,在角度接近0时(时间变化很小时近似角度为0),四元数近似为\([1, \Delta \phi_{\mathcal{L}} ]\)。
\[ \begin{aligned} \dot{\mathbf{q}} & \triangleq \lim _{\Delta t \rightarrow 0} \frac{\mathbf{q}(t+\Delta t)-\mathbf{q}(t)}{\Delta t} \\ &=\lim _{\Delta t \rightarrow 0} \frac{\mathbf{q} \otimes \Delta \mathbf{q}_{\mathcal{L}}-\mathbf{q}}{\Delta t} \\ &=\lim _{\Delta t \rightarrow 0} \frac{\mathbf{q} \otimes\left(\left[\begin{array}{c}{1} \\ {\Delta \boldsymbol{\phi}_{\mathcal{L}} / 2}\end{array}\right]-\left[\begin{array}{l}{1} \\ {\mathbf{0}}\end{array}\right]\right)}{\Delta t} \\ &=\lim _{\Delta t \rightarrow 0} \frac{\mathbf{q}(t+\Delta t)-\mathbf{q}(t)}{\Delta t} \\=& \frac{1}{2} \mathbf{q} \otimes\left[\begin{array}{c}{0} \\ {\boldsymbol{\omega}_{\mathcal{L}}}\end{array}\right] \end{aligned} \]
上式中:
\[ \omega_{\mathcal{L}}(t) \triangleq \frac{d \phi_{\mathcal{L}}(t)}{d t} \triangleq \lim _{\Delta t \rightarrow 0} \frac{\Delta \phi_{\mathcal{L}}}{\Delta t} \]
是旋转向量对时间的导数,可以理解为角速度向量 ## 使用Eigen库 Eigen库是一个开源的c++线性代数库,提供了快速的有关矩阵的线性代数运算,还包括解方程的功能。同时它还提供了几何模块,可以表示旋转的多种表示方式,包括上面提到的旋转矩阵、旋转向量、四元数等等。
参考资料
[1] http://www.chrobotics.com/library/understanding-quaternions
[2] https://blog.csdn.net/zhuquan945/article/details/72784274
[3] 视觉slam十四讲