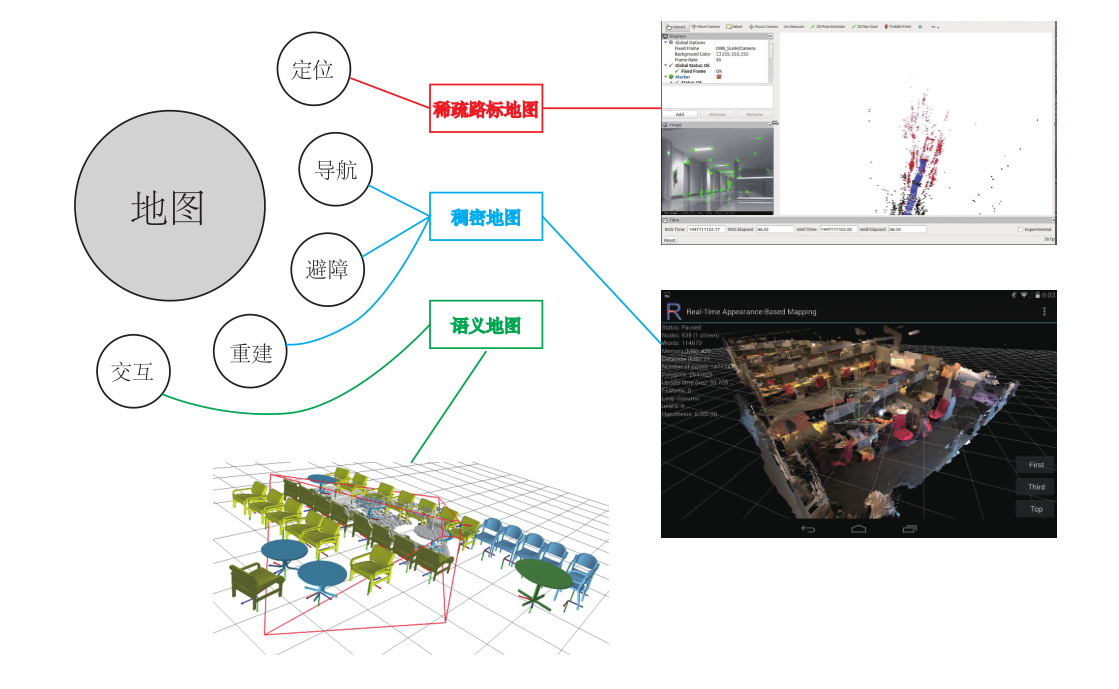
视觉slam中的一种单目稠密建图方法
slam是中文全名是同时定位与建图,但是大家更多关注的都是slam的定位作用,而对于建图,也许是因为三维重现、sfm之类的研究方向已经很多了,所以在slam大家对其的关注小了很多。本文主要就是简单讲解一下slam中进行单目稠密建图的一个思路。
之所以只讲单目的稠密建图,这是因为,首先,对于RGBD图,我们已知所有点的深度,可以直接生成稠密的点云,可讲的东西不多(其实还是很多的,但我现在了解的还不多)。其次,对于稀疏地图,其实很多VO中已经完成了稀疏地图的构建,但是稀疏地图只能用于定位,不能用于导航避障之类的工作。所以很多slam系统中会额外进行稠密地图、甚至语义地图的构建。
单目稠密建图
通常在单目VO中,我们通过特征点匹配与三角测量可以获得稀疏地图点的深度,现在我们想要建立稠密的地图,这意味着我们需要获得图片中所有像素点的深度。那么首先我们需要做的一点就是确定第一幅图的某个像素出现在其他图中的位置。此时我们当然可以遍历所有的像素点,然后计算所有像素点的描述子,然后在另一幅图片中寻找与其匹配的点。但是,这种方法先不说效果如何,光想想每一幅图像我们需要计算与匹配的特征描述子数量就够吓人的了。所以这种方法应该是不可取的。
针对这个问题,一种比较有效的方法是使用极线搜索与块匹配技术。
极线搜索与块匹配
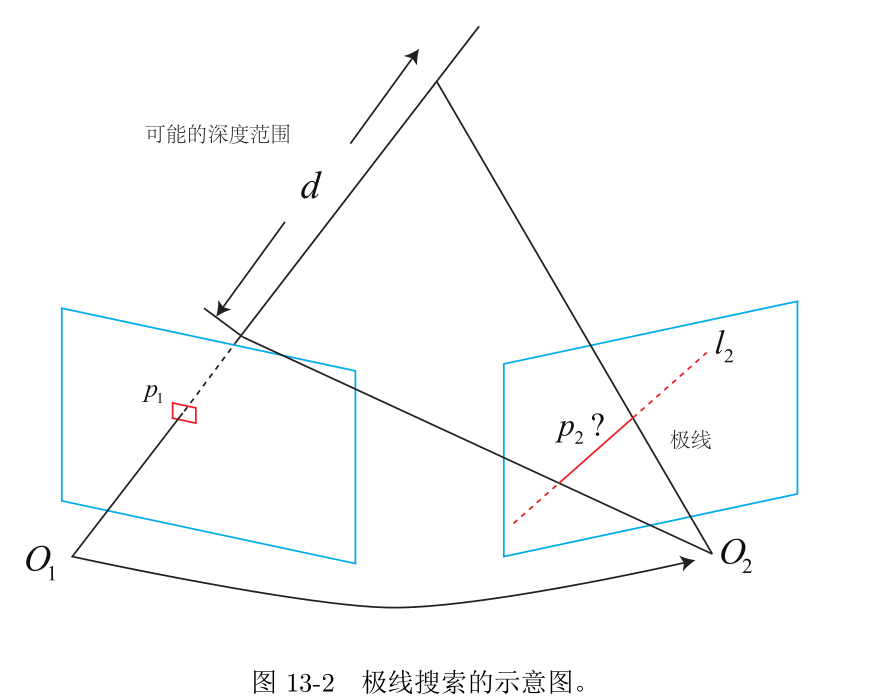
首先,在slam中建图,我们是可以使用前端的测量结果的,所以我们知道每一帧的相机位姿,也就是相机的外参,根据相机的外参与内参,我们可以将基准帧上的一点\(p\)(我们也称该点为种子)投影到当前帧的一条射线上,这条线也叫做极线(具体原理可以参考对极几何)。所以我们想找的点就在这条极线上,而在极线上确定这个点的过程就叫做极线搜索。
只要知道了两帧之间的相对位姿就可以确定极线,不过如果还知道点的初始深度,此时还可以缩小找匹配时的搜索量。
确定极线的方法有很多,我们在这里介绍一种\(svo\)中确定极线的方法:
在种子\(p(x,y)\)的深度延长线上,构造两个三维点\(P_{1}\)与\(P_{2}\),这两个三维点来源自同一个像素,只是确定它们的深度不同。在深度滤波器中一般是设置为
P1(x,y,z-n*sigma)与P2(x,y,z+n*sigma),其中\(z\)是种子的初始深度,\(sigma\)是深度的方差,\(n\)可以调节成不同的值,比如\(1,2,3...\)等,一般取\(3\)。将\(P_{1}\)与\(P_{2}\)利用帧间位姿,投影到当前帧,投影点为\(u_{1}\)与\(u_{2}\),连接\(u_{1}\)与\(u_{2}\)就是我们所要的极线(此处是一个线段)
块匹配
其实极线搜索我们一般都是采用了块匹配的方式。所谓的块匹配就是说对于极线上的一个点,我们判断它与参考点的相关性,是通过在点周围取一个\(w \times w\)的小块,然后在基线上也取很多同样大小的小块进行比较。比较的方法有很多,主要是衡量两个小块的相似性。
此处,我们假设对于一个像素点\(p_{1}\),我们将其周围的小块记成\(\boldsymbol{A} \in \mathbb{R}^{w \times w}\),把极线上的每个点的小块记为\(\boldsymbol{B}_{i}, i=1, \dots, n\)。那么,下列方法都可以用来计算小块之间的差异。
- SAD(Sum of Absolute Difference)。取两个小块的差的绝对值之和(这个结果越大,说明越不匹配,越接近0,块的相似度越高):
\[ S(\boldsymbol{A}, \boldsymbol{B})_{S A D}=\sum_{i, j}|\boldsymbol{A}(i, j)-\boldsymbol{B}(i, j)| \]
- SSD(Sum of Squared Distance)。即取两个小块的差的平方和(这个结果越大,说明越不匹配,越接近0,块的相似度越高):
\[ S(\boldsymbol{A}, \boldsymbol{B})_{S S D}=\sum_{i, j}(\boldsymbol{A}(i, j)-\boldsymbol{B}(i, j))^{2} \]
- NCC(Normalized Cross Correlation)。即计算两个小块的归一化互相关(这个结果越大,说明相似度越高,0时代表完全不相关):
\[ S(\boldsymbol{A}, \boldsymbol{B})_{N C C}=\frac{\sum_{i, j} \boldsymbol{A}(i, j) \boldsymbol{B}(i, j)}{\sqrt{\sum_{i, j} \boldsymbol{A}(i, j)^{2} \sum_{i, j} \boldsymbol{B}(i, j)^{2}}} \]
上述三种方法是比较常见的三种方法,现实中我们使用的方法可能要更复杂一点,比如在\(svo\)中使用的是\(ZMSSD\)对\(8 \times 8\)的矩形\(patch\)计算相似性,与此同时,通常我们在计算小块的差异之前,还需要做一些预处理操作,比如去均值(减小亮度影响)、根据参考帧与当前帧间的运动首先将块进行对应的仿射变换再进行匹配等。
深度滤波器
在使用极线搜索与块匹配确定了匹配的像素之后,使用三角测量便可以确定出该点的深度。但是我们知道,测量出来的像素也许是有噪声的,所以单次测量出来的深度其实是一个不确定值,我们可以假设它服从一种概率分布(lsd中假设为高斯分布),通过对于多帧不断的进行上述操作,我们可以尝试对测量出来的深度进行优化。这样,如何估计每个像素点的深度就变成了一个状态估计的问题,此时会存在滤波器与非线性优化两种求解的思路。
我们当然可以直接构造非线性最小二乘,然后使用非线性优化的方法进行求解,但是要知道我们是对整幅图像的所有像素进行深度估计,这样做计算量会很大,因此很多稠密建图的工作都是使用滤波器的方法更新深度,其中\(LSD\)使用的是卡尔曼滤波器,\(SVO\)提出了一种深度滤波器的方法。有时间会详细介绍这种方法。
常见问题与改进
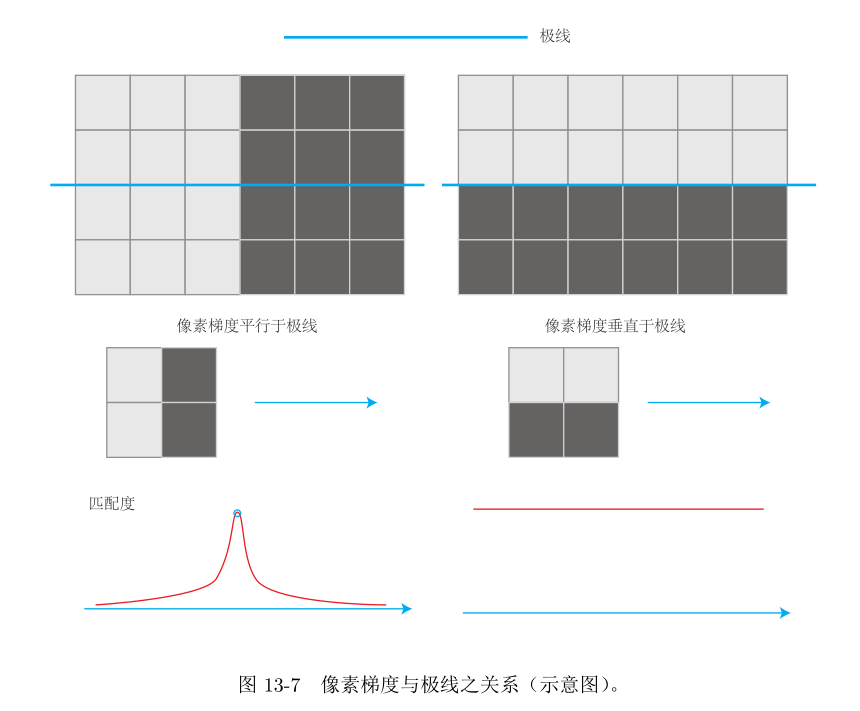
- 使用块匹配的方法很依赖图像环境,比如梯度明显的小块可能比较好区分,梯度不明显的像素容易引起误匹配。
在深度滤波器中假设深度满足高斯分布其实是不合理的,因为深度通常不像是高斯分布是一个对称的分布,而是一边短(因为深度不会小于相机焦距,近似0),一边长(深度可以是很深甚至无穷远),所以我们可以采用逆深度的概念,即假设深度的倒数(即将\(d\)改为\(d^{-1}\))为高斯分布,这样会得到更好的结果。
假设相机发生了旋转,那么块的相似性很难保持(比如上黑下白的图像库旋转会变成上白下黑),所以我们需要计算仿射矩阵(通过三点法确定),通过仿射矩阵将基准帧中的块\(A\)里的像素坐标逐一映射到当前帧中,这样映射的所有坐标就组成了块\(B\)。
由上面的介绍,我们会发现对每个像素的深度估计的过程都是相同但是独立的,因此我们可以并行的处理他们。GPU编程会比较适合。
使用统计滤波器去除孤立点。(统计每个点与它最近的N个点的距离值分布,去除距离均值过大的点)
使用体素滤波器去除重叠点。因为我们重建是基于很多图片,不可避免一个点可能在好多图片都观察到了,此时体素滤波器保证在某一个一定大小的立方体(也叫体素)内仅有一个点,相当于对三维空间进行了降采样,从而节省存储空间。体素滤波器可以根据不同的需求设置不同的分辨率
参考文献
- [1] 视觉slam十四讲