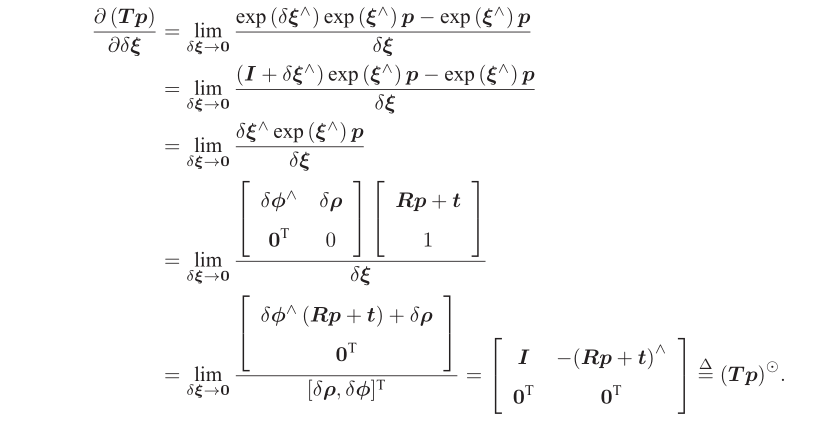李代数求导与扰动模型

\(SO(3)\)李代数上的扰动模型求导是slam中使用最广泛的公式。！！！

在上一篇博客中我们了解了李群与李代数的定义，那么知道这些有什么用呢？

我们经常构建与位姿有关的函数，然后讨论该函数关于位姿的导数，以调整当前的估计值。表示姿态的李群\(SO(3)\)与表示位姿的李群\(SE(3)\)上并没有定义加法，而求导数是需要加法的。因此此时如何求导就成了一个需要解决的问题，它们的李代数由向量组成，具有良好的加法运算，因此我们可以利用李代数来解决对位姿的求导问题。

\[ \begin{equation} \mathbf{R}(t) = \exp \left( \mathbf{\phi} (t) ^\wedge \right) \mathbf{R}(t_0) \end{equation} \]

上面看到了，因为SO(3)上没有定义加法，所以我们不能求R的导数。但是我们上一节中可以用\(\mathfrak{so}(3)\)通过指数映射来得到SO(3)，所以我们可以将求李代数的导数。

BCH公式

但是此处必须说明的一点是，指数映射时，下式是不满足的。

\[ \begin{equation} \exp \left( {\phi _1^ \wedge } \right)\exp \left( {\phi _2^ \wedge } \right) = \exp \left( {\left( {\phi _1} + {\phi _2} \right)}^ {\wedge } \right) \end{equation} \]

如果上述公式中\({\phi^ \wedge }\)是标量的话，那么肯定是成立的，但是很遗憾，它是一个矩阵。所以，它到底是什么呢？这需要用到BCH(Baker-Campbell-Hausdorff)公式。完整形式比较复杂，我们此处就不贴出了，直接上有用的。

\[ R_1 R_2 = \textbf{exp}({\phi_1}^{\wedge})\textbf{exp}({\phi_2}^{\wedge}) \approx \begin{equation} \begin{cases} \textbf{exp}(( J_l(\phi_2)^{-1} \phi_1 + \phi_2 )^{\wedge}) & \textbf{if } \phi_1 \textbf{ is small}\\ \textbf{exp}(( J_r(\phi_1)^{-1} \phi_2+ \phi_1 )^{\wedge}) & \textbf{if } \phi_2 \textbf{ is small} \end{cases} \end{equation} \]

其中，第一个称为左乘模型，第二个称为右乘模型。

\(J_l\)即\(\mathfrak{se}(3)\)到\(SE(3)\)转换时求得的J，称为左乘近似雅可比:

\[ J_l = J=\dfrac{\sin \theta}{\theta} I + (1- \dfrac{\sin \theta}{\theta})aa^T + \dfrac{1-\cos \theta}{\theta}a^{\wedge} \]

它的逆为:

$$ J_l^{-1} = I + (1- )aa^T - a^{} $

而右乘雅可比仅需要对自变量取负号即可:

\[ J_r(\phi)=J_l(-\phi) \]

此时，如果将上面的结果反过来，在李代数上做加法，则有（最有用的）:

\[ \textbf{exp}((\phi+ \Delta\phi)^{\wedge}) = \textbf{exp}((J_l \Delta\phi)^{\wedge}) \textbf{exp}({\phi}^{\wedge})=\textbf{exp}({\phi}^{\wedge})\textbf{exp}((J_r \Delta\phi)^{\wedge}) \]

在\(\mathfrak{se}(3)\)上的运算与\(\mathfrak{so}(3)\)类似，只是雅可比矩阵的求法稍有不同。其实我们发现上面的左乘雅克比与右乘雅克比都有些复杂，其实下面我们会发现，如果使用扰动模型进行求导根本用不到它们！因此这里直接跳过它们的内容求解。

基于李代数对姿态求导

本来我们想求得是

\[ \frac{d\left( {RP} \right)}{dR} = \mathop {\lim }\limits_{\Delta R \to 0} \frac{\left( {R + \Delta R} \right)P - RP}{\Delta R} \]

但是，\(R+\Delta R\)不再是旋转矩阵。因此我们需要另想办法。有了上面的工作，下面我们就可以完成基于李代数的求导操作了，此处介绍两种模型，因为扰动模型的形式会简单一些，因此大家一般都是使用扰动模型，微分模型也了解一下 ## 利用BCH公式的微分模型求导 ### \(SO(3)\)李代数上的微分模型 > 用李代数表示姿态，然后根据李代数加法来对李代数求导。即传统求导的思路，把增量直接定义在李代数上。

\[ \begin{aligned} \frac{\partial\left(\exp \left(\phi^{\wedge}\right) \boldsymbol{p}\right)}{\partial \phi} &=\lim _{\delta \phi \rightarrow 0} \frac{\exp \left((\phi+\delta \phi)^{\wedge}\right) \boldsymbol{p}-\exp \left(\phi^{\wedge}\right) \boldsymbol{p}}{\delta \phi} \\ &=\lim _{\delta \phi \rightarrow 0} \frac{\exp \left(\left(\boldsymbol{J}_{l} \delta \phi\right)^{\wedge}\right) \exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}-\exp \left(\phi^{\wedge}\right) \boldsymbol{p}}{\delta \phi} \\ &=\lim _{\delta \phi \rightarrow 0} \frac{\left(\boldsymbol{I}+\left(\boldsymbol{J}_{l} \delta \boldsymbol{\phi}\right)^{\wedge}\right) \exp \left(\phi^{\wedge}\right) \boldsymbol{p}-\exp \left(\phi^{\wedge}\right) \boldsymbol{p}}{\delta \phi} \\ &=\lim _{\delta \phi \rightarrow 0} \frac{\left(\boldsymbol{J}_{l} \delta \boldsymbol{\phi}\right)^{\wedge} \exp \left(\phi^{\wedge}\right) \boldsymbol{p}}{\delta \phi}=-(\boldsymbol{R} \boldsymbol{p})^{\wedge} \boldsymbol{J}_{l} \\ &=\lim _{\delta \phi \rightarrow 0} \frac{-\left(\exp \left(\phi^{\wedge}\right) \boldsymbol{p}\right)^{\wedge} \boldsymbol{J}_{l} \delta \phi}{\delta \phi}=-(\boldsymbol{R} \boldsymbol{p})^{\wedge} \boldsymbol{J}_{l} \end{aligned} \]

上面第四行到第五行将反对称符号看做叉乘，变换之后变号，并且微分模型的结果最后需要计算一个雅可比矩阵，要麻烦一些，所以实际工程中很少使用这种方式。下面的扰动模型其实才是工程中广泛使用的方法。

扰动模型求导

对李群左乘或者右乘微小扰动，然后对该扰动求导，称为左扰动和右扰动模型。即把增量扰动直接添加在李群上，然后使用李代数表示此扰动

\(SO(3)\)李代数上的扰动模型(左扰动) !!! 这是slam中应用最多的公式

\[ \begin{aligned} \frac{\partial(\boldsymbol{R} \boldsymbol{p})}{\partial \boldsymbol{\varphi}} &=\lim _{\varphi \rightarrow 0} \frac{\exp \left(\boldsymbol{\varphi}^{\wedge}\right) \exp \left(\phi^{\wedge}\right) \boldsymbol{p}-\exp \left(\phi^{\wedge}\right) \boldsymbol{p}}{\varphi} \\ &=\lim _{\varphi \rightarrow 0} \frac{\left(\boldsymbol{I}+\boldsymbol{\varphi}^{\wedge}\right) \exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}-\exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}}{\varphi} \\ &=\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{\boldsymbol{\varphi}^{\wedge} \boldsymbol{R} \boldsymbol{p}}{\varphi}=\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{-(\boldsymbol{R} \boldsymbol{p})^{\wedge} \boldsymbol{\varphi}}{\varphi}=-(\boldsymbol{R} \boldsymbol{p})^{\wedge} \end{aligned} \]

这一种方法直接将小量乘在李群上，而不是李代数上。并且需要注意的是这种模型需要区别是左乘还是右乘。左扰动模型比微分模型要少一个雅可比矩阵。

\(SE(3)\)上的扰动模型

含义是：考虑一个空间点P（需要是齐次坐标，否则维数不对），受到刚体变换T，得到\(TP\)。下面要求解\(TP\)是如何随着T变化的。

\[ \begin{equation} \begin{aligned} \dfrac{\partial(\textbf {TP})}{\partial T} &= \lim_{\delta \xi \rightarrow 0} \dfrac{\textbf{exp}((\delta \xi)^{\wedge}) \textbf TP-\textbf TP}{\delta \xi} \\ &= (TP)^{\odot} \end{aligned} \end{equation} \]

其中，\(^ \odot\)将一个4×4的矩阵变换成一个4×6的矩阵

假设如下求导中左乘的扰动项的李代数为\(\delta \boldsymbol{\xi}=[\delta \boldsymbol{\rho}, \delta \phi]^{\mathrm{T}}\)，那么：

上面最后一行矩阵除法，与矩阵乘法规则类似，只是乘号变成了除号。其使用一个\(4×1\)矩阵除以一个\(1×6\)矩阵得到一个\(4×6\)矩阵

总结

我们讲解了如何对位姿进行求导，这是后面对位姿进行非线性优化的基础。

引入李群李代数的意义：第一个是因为在欧式变换矩阵上不好定义导数，引入李群李代数使得导数定义变得自然合理；第二个是本来旋转矩阵与欧式变换矩阵具有本身的约束，使得将它们作为优化变量会引入额外约束，通过李群李代数可以使得问题变成一个无约束的优化问题。

参考文献

• [1]. https://zhehangt.github.io/2017/03/16/SLAM/Basic/LieAlgebra-02/
• [2]. 视觉SLAM十四讲-从理论到实践