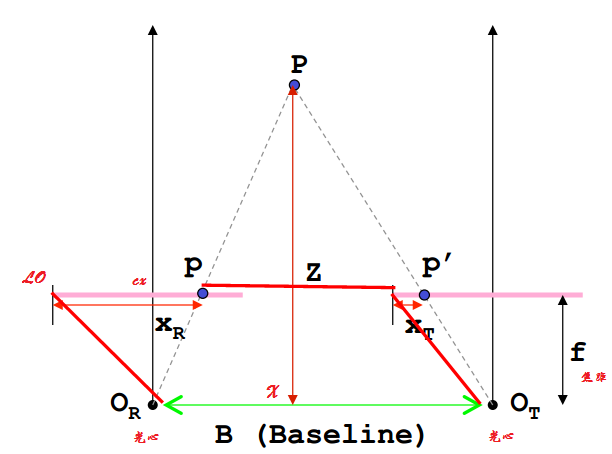
单目vo中的深度确定方法--三角测量

三角测量的目的是用来确定图片中某一个点的深度。为什么会有这样的需求呢？我们在前面的博客中提到了对极几何与单应变换。在前面其实已经提到过了，在单目VO中，虽然我们可以通过本质矩阵与单应矩阵恢复出相机变换的位姿，但是这两种方法确定的位姿变换是具有尺度不确定性的。在双目vo中，我们会首先使用三角测量恢复出深度信息，再进行位姿估计。

因为基础矩阵与单应矩阵本身描述的是从一个2d平面到另一个2d平面的变换，无需3d深度信息，这两种变换都是正常进行的，因此自然就具有尺度不确定性。更加具体的讲，将基础矩阵与单应矩阵作用在一个齐次坐标(x,y,1)上时，此时，随意的将基础矩阵与单应矩阵进行一定尺度缩放，由于齐次坐标的尺度等价性，对最终的变换结果都不会产生影响。

三角测量

三角测量本身是由高斯提出，最早应用在天文地理领域，根据不同季节观察到的星星的角度，估计星星与我们的距离。

在相机几何中的应用，推导如下：

注意，三角测量依据的是同一个空间点在不同时刻的投影到相机成像平面上的位置来确定这两个时刻时这个点的深度。

第一种思路

由相机成像的几何描述我们可以理解如下的公式(世界坐标到像素坐标的转换)：

\[ Z_1p_{uv1} = K_1P_w \]

\[ Z_2p_{uv2} = K_2(RP_w + t) \]

其中K是相机内参，R与t是第二个相机在第一个相机的相机坐标系下的外参，\(P_w\)是此空间点在第一个相机的相机坐标系下的坐标。Z是空间点到相机光心的距离(也是相机坐标系下的z轴坐标)。\(p_{uv1}\)与\(p_{uv2}\)是空间点\(P_w\)在两个相机平面上的投影点。

• 首先做出如下定义（其中\(x_1\)与\(x_2\)是归一化的相机坐标（X/Z,Y/Z,1））：

\[ x_1 = K_1^{-1}p_{uv1} \]

\[ x_2 = K_2^{-1}p_{uv2} \]

• 带入如上定义可得：

\[ Z_2 x_2 = Z_1 Rx_1 + t \]

• 由于我们已经通过本质矩阵分解或者单应矩阵分解获得了R与t，此时想求的是两个特征点的深度，即上式中的\(Z_1\)与\(Z_2\)，此时，可通过如下操作分别求出，首先求解\(Z_1\)，上式两边同时左乘x2^，也就是两侧同时与\(x_2\)做外积：

\[ Z_2 x_2^{\land} x_2 = 0 = Z_1 x_2^{\land}Rx_1 + x_1^{\land}t \]

如上，可以直接求出\(p_{uv1}\)的深度\(Z_1\)了，然后\(Z_1\)也可以很轻松地求出。

代码实现（自己实现）

首先是上述思路的解法

bool depthFromTriangulation(
    const SE3& T_search_ref,
    const Vector3d& f_ref,
    const Vector3d& f_cur,
    double& depth)
{
    Matrix<double,3,2> A;
    A << T_search_ref.rotation_matrix()*f_ref, f_cur;
    const Matrix2d AtA = A.transpose()*A;
    if(AtA.determinant() < 0.000001)
        return false;
    const Vector2d depth2 = - AtA.inverse()*A.transpose()*T_search_ref.translation();
    depth = fabs(depth2[0]);
    return true;
}

---

第二种思路

然后此处使用的求解方法是\(Cramer's\)法则。这是另一种求解三角化的方式，推导如下：

\[ Z_{2} x_{2} - Z_{1} Rx_{1} = t \]

对公式两侧同时乘以\(x_{2}^T\)，得到：

\[ Z_{2} x_{2}^T x_{2} - Z_{1} x_{2}^T R x_{1} = x_{2}^T t \]

公式两侧同时乘以\((Rx_{1})^T\)，得到：

\[ Z_{2} (Rx_{1})^T x_{2} - Z_{1} (Rx_{1})^T Rx_{1} = (Rx_{1})^Tt \]

对于上述两个公式组成的方程组，利用克莱默法则求解

\[ \left[ \begin{array}{cc}{\mathrm{x}_{2}^{T} x_{2}} & {-\mathrm{x}_{2}^{T} R x_{1}} \\ {\left(R x_{1}\right)^{\mathrm{T}} x_{2}} & {-\left(R x_{1}\right)^{\mathrm{T}}\left(R x_{1}\right)}\end{array}\right] \left[ \begin{array}{c}{Z_{2}} \\ {Z_{1}}\end{array}\right]=\left[ \begin{array}{c}{\mathrm{x}_{2}^{T} t} \\ {\left(R x_{1}\right)^{\mathrm{T}} t}\end{array}\right] \]

克莱默法则是，对于\(Ax=b\)这样的方程，如果\(A\)的行列式不为0，方程可以通过如下方式求解：

\[ x_{1}=\frac{\operatorname{det} B_{1}}{\operatorname{det} A} \quad x_{2}=\frac{\operatorname{det} B_{2}}{\operatorname{det} A} \quad x_{n}=\frac{\operatorname{det} B_{n}}{\operatorname{det} A} \]

其中\(B_{j}\)是\(A\)的第\(j\)列被\(b\)替换后得到的新的矩阵。

// 方程
    // d_ref * f_ref = d_cur * ( R_RC * f_cur ) + t_RC
    // => [ f_ref^T f_ref, -f_ref^T f_cur ] [d_ref] = [f_ref^T t]
    //    [ f_cur^T f_ref, -f_cur^T f_cur ] [d_cur] = [f_cur^T t]
    // 二阶方程用克莱默法则求解并解之
    Vector3d t = T_R_C.translation();
    Vector3d f2 = T_R_C.rotation_matrix() * f_curr; 
    Vector2d b = Vector2d ( t.dot ( f_ref ), t.dot ( f2 ) );
    // 此处计算出系数矩阵A
    double A[4];
    A[0] = f_ref.dot ( f_ref );
    A[2] = f_ref.dot ( f2 );
    A[1] = -A[2];
    A[3] = - f2.dot ( f2 );
    // 此处计算A的行列式
    double d = A[0]*A[3]-A[1]*A[2];
    Vector2d lambdavec = 
        Vector2d (  A[3] * b ( 0,0 ) - A[1] * b ( 1,0 ),
                    -A[2] * b ( 0,0 ) + A[0] * b ( 1,0 )) /d;
    Vector3d xm = lambdavec ( 0,0 ) * f_ref;
    Vector3d xn = t + lambdavec ( 1,0 ) * f2;
    Vector3d d_esti = ( xm+xn ) / 2.0;  // 三角化算得的深度向量
    double depth_estimation = d_esti.norm();   // 深度值

代码实现（使用opencv提供的接口）

void triangulation ( 
    const vector< KeyPoint >& keypoint_1, 
    const vector< KeyPoint >& keypoint_2, 
    const std::vector< DMatch >& matches,
    const Mat& R, const Mat& t, 
    vector< Point3d >& points )
{
    //相机第一个位置处的位姿
    Mat T1 = (Mat_<float> (3,4) <<
        1,0,0,0,
        0,1,0,0,
        0,0,1,0);
    //相机第二个位置处的位姿
    Mat T2 = (Mat_<float> (3,4) <<
        R.at<double>(0,0), R.at<double>(0,1), R.at<double>(0,2), t.at<double>(0,0),
        R.at<double>(1,0), R.at<double>(1,1), R.at<double>(1,2), t.at<double>(1,0),
        R.at<double>(2,0), R.at<double>(2,1), R.at<double>(2,2), t.at<double>(2,0)
    );
    
    // 相机内参
    Mat K = ( Mat_<double> ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
    vector<Point2f> pts_1, pts_2;
    for ( DMatch m:matches )
    {
        // 将像素坐标转换至相机平面坐标，为什么要这一步，上面推导中有讲
        pts_1.push_back ( pixel2cam( keypoint_1[m.queryIdx].pt, K) );
        pts_2.push_back ( pixel2cam( keypoint_2[m.trainIdx].pt, K) );
    }
    
    Mat pts_4d;
    //opencv提供的三角测量函数
    cv::triangulatePoints( T1, T2, pts_1, pts_2, pts_4d );
    
    // 转换成非齐次坐标
    for ( int i=0; i<pts_4d.cols; i++ )
    {
        Mat x = pts_4d.col(i);
        x /= x.at<float>(3,0); // 归一化
        Point3d p (
            x.at<float>(0,0), 
            x.at<float>(1,0), 
            x.at<float>(2,0) 
        );
        points.push_back( p );
    }
}

Point2f pixel2cam ( const Point2d& p, const Mat& K )
{
    return Point2f
    (
        ( p.x - K.at<double>(0,2) ) / K.at<double>(0,0), 
        ( p.y - K.at<double>(1,2) ) / K.at<double>(1,1) 
    );
}

代码地址

第三种思路（最小二乘法求解深度）

• 对于某个路标点y,在若干个关键帧\(k(0,1,2,...)\)中可以观测到

• 首先，对于\(\mathbf{y} \in \mathbb{R}^{4}\)，是空间点在世界坐标系中的齐次坐标。每次观测为\(x_{k} = \left[u_{k}, v_{k}, 1\right]^{T}\)，这个是相机成像平面的归一化坐标

• 我们假设投影矩阵为\(P_{k}=\left[R_{k}, \mathbf{t}_{k}\right] \in \mathbb{R}^{3 \times 4}\)，这个是从world系到camera系的投影

• 所以，投影关系为：

\[\forall k, \lambda_{k} \mathbf{x}_{k}=\mathbf{P}_{k} \mathbf{y}\]

其中\(\lambda_{k}\)为观测点的深度值

• 根据上面我们可以知道下式:

\[\lambda_{k}=\mathbf{P}_{k, 3}^{\top} \mathbf{y}\]

其中\(P_{k, 3}^{\top}\)是\(P_{k}\)的第三行（其中角标T仅仅代表是一个横向量）

• 我们再将上式带入投影变换的前两行，就得到：

\[ \begin{aligned} u_{k} \mathbf{P}_{k, 3}^{\top} \mathbf{y} &=\mathbf{P}_{k, 1}^{\top} \mathbf{y} \\ v_{k} \mathbf{P}_{k, 3}^{\top} \mathbf{y} &=\mathbf{P}_{k, 2}^{\top} \mathbf{y} \end{aligned} \]

• 每次观测都可以提供两个这样的方程，将y看做未知量，并将其移到等式一侧，可以得到下式：

\[ \left[\begin{array}{c}{u_{1} \mathbf{P}_{1,3}^{\top}-\mathbf{P}_{1,1}^{\top}} \\ {v_{1} \mathbf{P}_{1,3}^{\top}-\mathbf{P}_{1,2}^{\top}} \\ {\vdots} \\ {u_{n} \mathbf{P}_{n, 3}^{\top}-\mathbf{P}_{n, 1}^{\top}} \\ {v_{n} \mathbf{P}_{n, 3}^{\top}-\mathbf{P}_{n, 2}^{\top}}\end{array}\right] \mathbf{y}=\mathbf{0} \rightarrow \mathbf{D y}=\mathbf{0} \]

• 于是，y为D零空间的一个非零元素。

最小二乘求解

对于上面问题，由于\(\mathbf{D} \in \mathbb{R}^{2 n \times 4}\)，在观测时往往是大于等于两次的，很有可能D满秩（4），也就是无零空间。

• 此时我们会寻找上式的最小二乘解：

\[ \min _{\mathbf{y}}\|\mathbf{D} \mathbf{y}\|_{2}^{2}, \quad \text { s.t. }\|\mathbf{y}\|=1 \]

• 求解上述这个最小二乘问题\(y^{T}D^{T}Dy\)，我们可以通过对\(D^{T}D\)进行奇异值分解来求解。

\[ \mathbf{D}^{\top} \mathbf{D}=\sum_{i=1}^{4} \sigma_{i}^{2} \mathbf{u}_{i} \mathbf{u}_{j}^{\top} \]

• 其中\(\sigma_{i}\)为奇异值，并且会由大到小排列（它们对应的特征向量是一组单位正交基），我们找到最小（后面）的那个奇异值，它对应的特征向量，将其转换为齐次坐标，前三维就是y坐标的解了。

通常我们求出来会验证一下该解的有效性，判断条件是\(\sigma_{4} \ll \sigma_{3}\)。若该条件成立，则认为三角化有效。

代码

// vins中初始化sfm时根据一个三维点在两帧中的投影位置确定三维点位置
void GlobalSFM::triangulatePoint(Eigen::Matrix<double, 3, 4> &Pose0, Eigen::Matrix<double, 3, 4> &Pose1,
						Vector2d &point0, Vector2d &point1, Vector3d &point_3d)
{
	Matrix4d design_matrix = Matrix4d::Zero();
	design_matrix.row(0) = point0[0] * Pose0.row(2) - Pose0.row(0);
	design_matrix.row(1) = point0[1] * Pose0.row(2) - Pose0.row(1);
	design_matrix.row(2) = point1[0] * Pose1.row(2) - Pose1.row(0);
	design_matrix.row(3) = point1[1] * Pose1.row(2) - Pose1.row(1);
	Vector4d triangulated_point;
	triangulated_point =
		      design_matrix.jacobiSvd(Eigen::ComputeFullV).matrixV().rightCols<1>();
	point_3d(0) = triangulated_point(0) / triangulated_point(3);
	point_3d(1) = triangulated_point(1) / triangulated_point(3);
	point_3d(2) = triangulated_point(2) / triangulated_point(3);
}

使用概率方法更新矫正深度值

从上述讲述中，我们已经知道通过两帧图像的匹配点，可以得到一个等式，可以计算出这一点的深度值，所以，如果有n副图像进行匹配，那我们会得到n-1个等式。此时我们就可以计算出这一点的n-1个空间位置的测量值。

好的测量值是符合正太分布的，噪声符合均匀分布，此时我们可以通过一些概率的方法对多次测量结果进行融合，得到更鲁棒的结果。

• 在SVO中，使用贝叶斯方法(最大后验概率)进行更新

• 在LSD中，使用卡尔曼滤波进行深度测量值的滤波

其他测距方法

1. 主动方法
   • 结构光: 光已知空间方向的投影光线的集合称为结构光，结构光激光散斑通过投射具有高度伪随机性的激光散斑，会随着不同距离变换不同的图案，对三维空间直接标记，通过观察物体表面的散斑图案就可以判断其深度。
   • ToF: 飞行时间法，通过连续发射光脉冲（一般是不可见光），到被观测物体上，然后接收从物体反射回去的光脉冲，通过探测光脉冲的往返飞行时间来计算被测物体距离。
   • LIDAR: 激光雷达
2. 使用深度学习构建神经网络对图像深度进行预测

参考文献

• [1] 《视觉slam十四讲》
• [2] https://ewenwan.github.io