排序算法总结
排序问题是一个基础问题,这篇博客主要总结一下各种经典常用的有特色的排序算法。
冒泡排序(bubble sort)
原理:每次从左向右两两进行比较,将较大/小的交换到后面。每一个循环可以确定排好一个数,循环n-1次,完全排序完毕。
1
2
3
4
5
6
7
8
9
10
11
void bubble_sort(vector<int> & nums){
for(int i=0; i<nums.size()-1; ++i){
for(int j=0; j<nums.size()-1-i; ++j){
if(nums[j]>nums[j+1]){
int temp = nums[j];
nums[j] = nums[j+1];
nums[j+1] = temp;
}
}
}
}
1 | |
复杂度分析:重复
n-1次循环,每次循环比较平均n/2步,因此时间复杂度是o(n^2),空间复杂度是o(n)
插入排序(Insertion sort)
原理:循环n-1次,每次将当前的(从1开始)数插入到前面已经排序完毕序列中合适的位置。
1
2
3
4
5
6
7
8
9
void insert_sort(vector<int> &nums){
for(int i=1; i<nums.size(); ++i){
for(int j=i; j>0 && nums[j]<nums[j-1]; --j){
int temp = nums[j];
nums[j] = nums[j-1];
nums[j-1]= temp;
}
}
}
1 | |
复杂度分析: 重复
n-1次循环,每次循环平均n/4步,因此时间复杂度是o(n^2),空间复杂度是o(n)
选择排序(selection sort)
原理: 每次从乱序数组中找处最大(小)的那个值,将其放在当前乱序数组的头部,最终使得数组有序
1
2
3
4
5
6
7
8
9
10
11
void selection_sort(vector<int> &nums){
for(int i=0; i<nums.size()-1; ++i){
int min=i;
for(int j=i+1; j<nums.size(); ++j){
if(nums[j]<nums[min]) min=j;
}
int temp = nums[i];
nums[i] = nums[min];
nums[min] = temp;
}
}
1 | |
复杂度分析: 重复
n-1次循环,每次循环平均n/2步,因此时间复杂度是o(n^2),空间复杂度是o(n)
希尔排序(shell sort)
插入排序的改进版,是一种非稳定排序算法。插入排序的特点: 1. 插入排序在对几乎已经排好序的数据操作时,效率高,可以达到线性排序的效率 2. 但一般情况下,插入排序是低效的,因此每次只将数据移动一位
希尔排序通过多次插入排序,提升插入排序的性能,实例如下:
对于一组数
13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10首先设置步长为5,则这组数可以如下表示,一共将数据分成了5组
1
2
3
413 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10然后对于每组(列)进行插入排序,得到
1
2
3
413 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10上述数组现在变为
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45此时设置步长为3,将数据分成了3组
1
2
3
4
5
610 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45对上述每组(列)进行插入排序,得到
1
2
3
4
5
610 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94最后再以1为步长进行插入排序,就可以得到正确结果了。
希尔排序无论初始步长是多少,也无论中间步长是多少,只要最后一遍步长为1,最后的结果就肯定是正确的。前面那么多次的排序只是为了减少最后一次排序的时间。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//此处步长设置为每次2倍递减
void shell_sort(vector<int> &nums)
{
for (int gap = nums.size() >> 1; gap > 0; gap >>= 1) {
for (int i = gap; i < nums.size(); i++) {
int temp = nums[i];
int j = i - gap;
for (; j >= 0 && nums[j] > temp; j -= gap) {
nums[j + gap] = nums[j];
}
nums[j + gap] = temp;
}
}
}
1 | |
复杂度分析:希尔排序的复杂度与步长选择有很大关系,最坏情况为
o(n^2),最好复杂度为o(n(logn)^2),目前已知最好步长序列是(1,5,19,41,109,...)
归并排序(merge sort)
原理:采用分冶思想,首先将数组不断二等分成小数组,然后合并小数组进行排序。具体过程可以参考下图
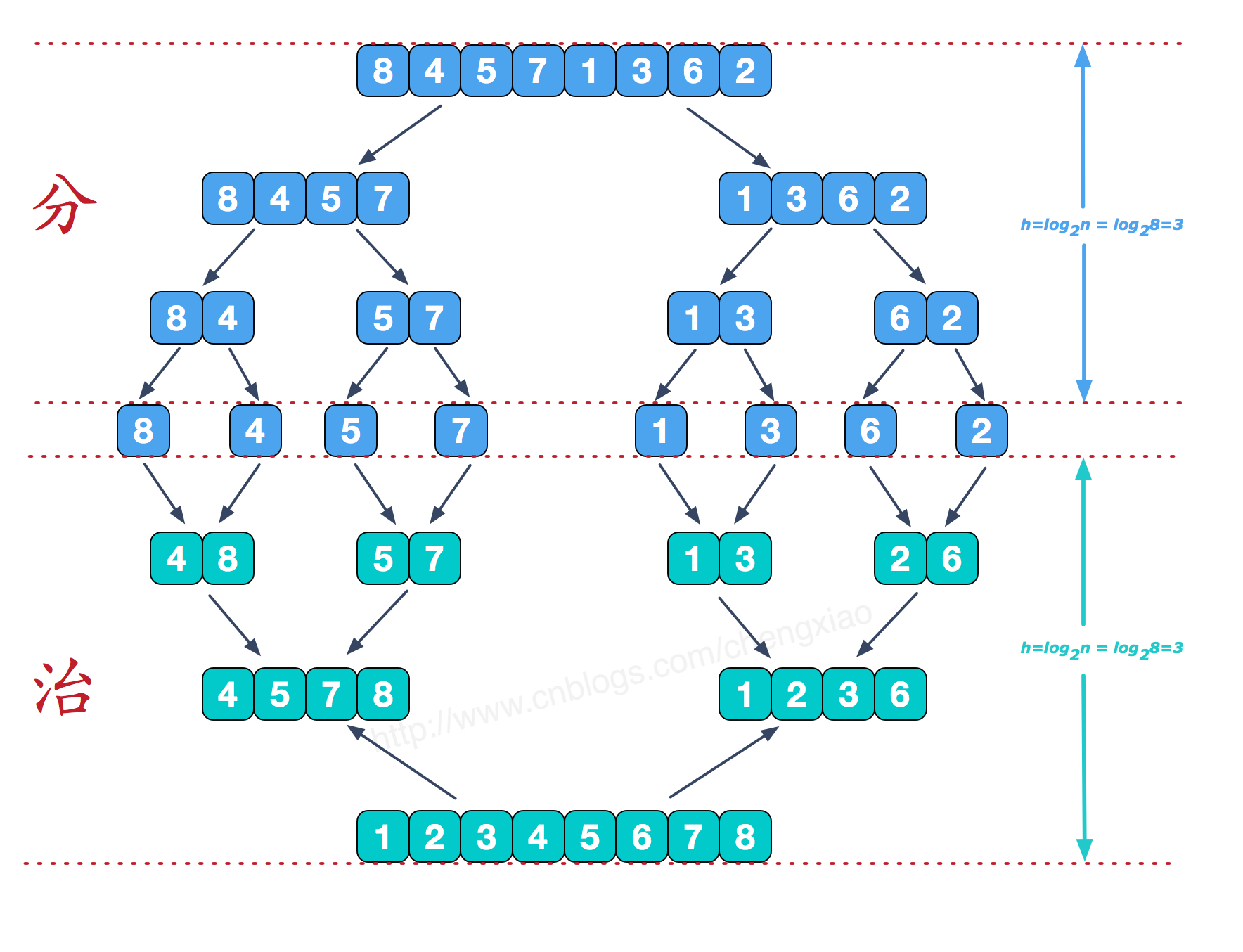
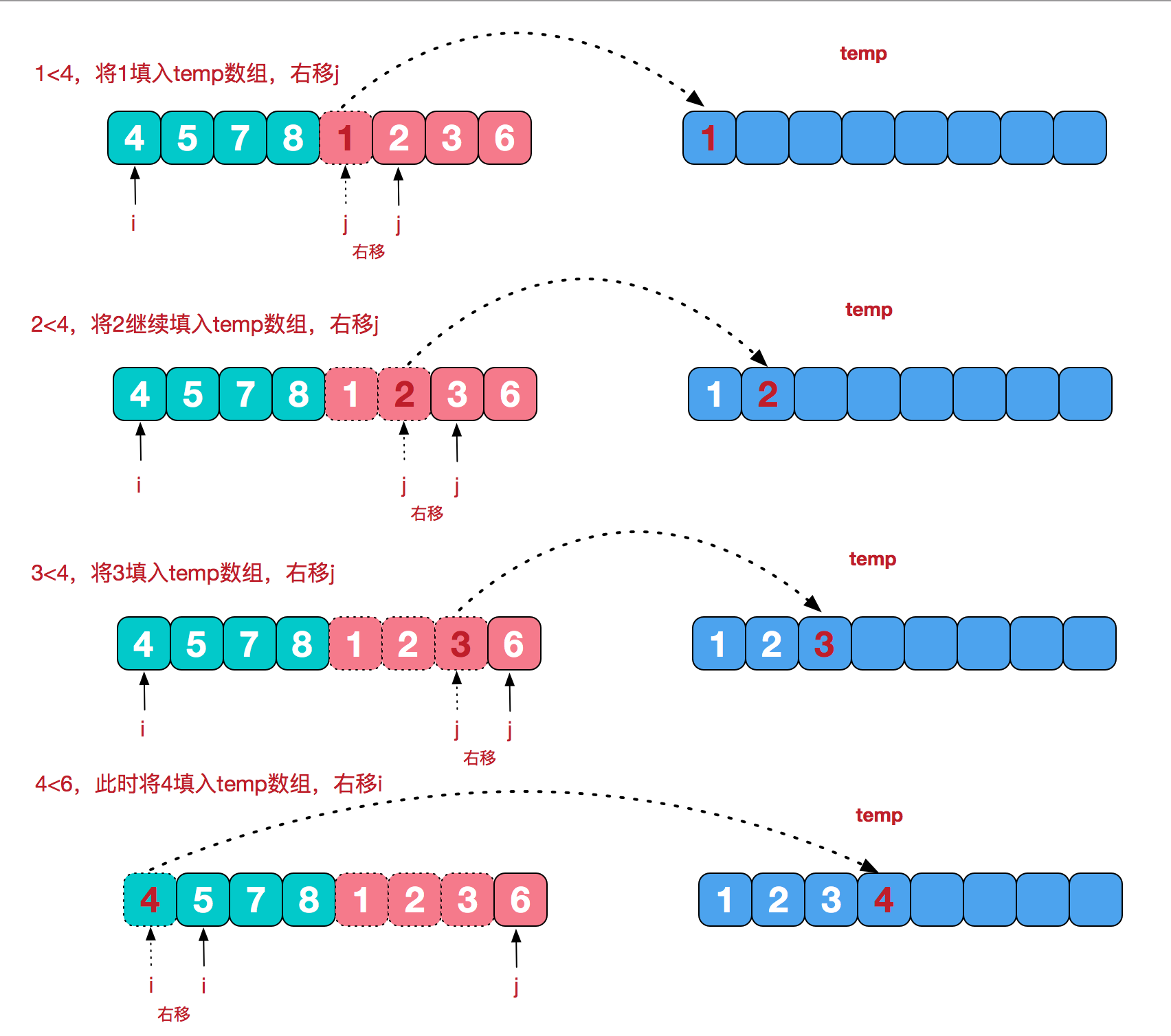
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
void merge_sort(vector<int> &nums){
int size = nums.size();
vector<int> temp(size);
merge_sort(nums, 0, size-1, temp);
}
void merge_sort(vector<int> &nums, int b, int e, vector<int> &temp){
if(b<e){
int m = (b+e)/2;
merge_sort(nums, b, m, temp);
merge_sort(nums, m+1, e, temp);
merge(nums, b, m, e, temp);
}
}
void merge(vector<int> &nums, int b, int m, int e, vector<int> &temp){
int i=b;
int j=m+1;
int t=0;
while(i<=m && j<=e){
if(nums[i]<=nums[j]){
temp[t++]=nums[i++];
}
else temp[t++]=nums[j++];
}
while(i<=m){
temp[t++]=nums[i++];
}
while(j<=e){
temp[t++]=nums[j++];
}
t=0;
//将排序好的数拷贝到原数组
while(b<=e){
nums[b++]=temp[t++];
}
}
1 | |
评价:归并排序是稳定排序,它也是一种十分高效的排序。每次合并操作的平均时间复杂度是
o(n),而完全二叉树的深度是log_2(n),所以总的时间复杂度是o(nlogn)。归并排序的最好、最坏、平均时间复杂度都是o(nlogn)
快速排序(quick sort)
原理:快速排序也利用了分冶思想。它的做法是:每次选择一个基准数,将比基准数小的挪到左边,大的挪到右边。然后对左右两部分执行相同操作,直到有序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void quick_sort(vector<int> &nums){
int size = nums.size();
quick_sort(nums, 0, size-1);
}
void quick_sort(vector<int> &nums, int b, int e){
//每次以第一个元素作为基准数
if(b<e){
int l=b, r=e;
while(l<r){
while(nums[r]>=nums[b] && r>l) r--;
while(nums[l]<=nums[b] && l<r) l++;
swap(nums[r], nums[l]);
}
swap(nums[b], nums[l]);
quick_sort(nums, b, l);
quick_sort(nums, l+1, e);
}
}
1 | |
评价:快速排序是不稳定排序,平均时间复杂度是
o(nlogn),上面这种解法不需要辅助空间。
堆排序(heap sort)
堆是一种完全二叉树,大顶堆:每个节点的值都大于或等于其左右孩子节点的值。小顶堆:每个节点的值都小于或等于其左右孩子节点的值。如下: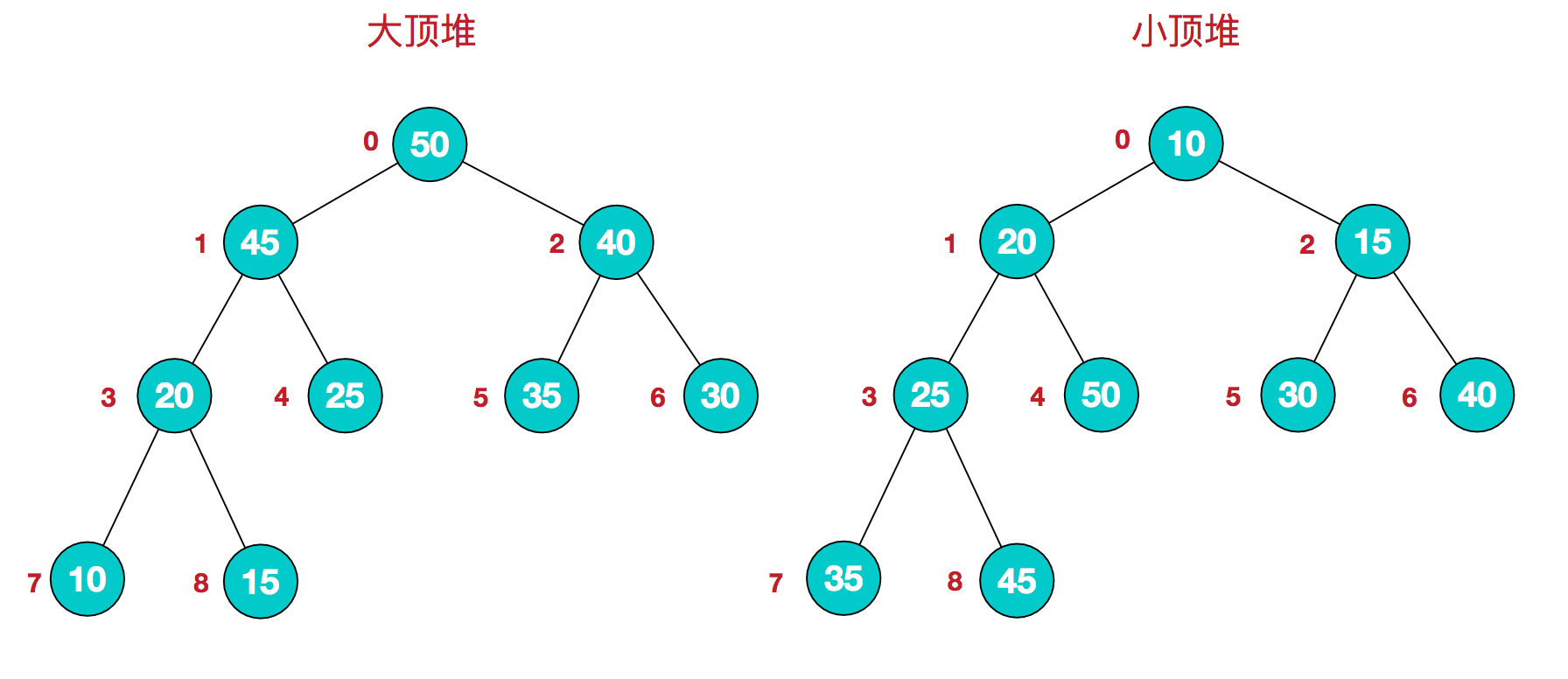
arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] 2.
小顶堆 :
arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

原理:利用堆这种数据结构进行排序,将待排序序列构造成一个大顶堆,此时整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个大顶堆,得到n-1个元素中的最大值...如此反复,就能得到一个有序序列了。
在一个数组上构造大顶堆时,只需要调整父节点就可以了(如果子节点中有比自己大的,选择最大的子节点与自己交换值)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29void heap_sort(vector<int> &nums){
//构建大顶堆
int size = nums.size();
for(int i=size/2-1; i>0; --i){
//从最后一个非叶子节点开始调整
heap_adjust(nums, i, size-1)
}
//交换堆顶与末尾元素并重新调整堆结构
for(int i=len-1; i>0; ++i){
swap(nums[0], nums[i]);
heap_adjust(nums, 0, i-1);
}
}
//这个函数是调整堆,只是为了服务上面函数,所以并不是一个完整的构造堆的函数
void heap_adjust(vector<int> &nums, int b, int e){
int father = i;
int son = 2*father+1;
while(son<=e){
if(son+1<=e && nums[son]<nums[son+1]) son++;
if(nums[father]<nums[son]){
swap(nums[father], nums[son]);
father=son;
son=2*father+1;
}
else break; //此处break是因为下面的本来是调整过的都,如果这一步已经满足了,下面就没有继续的必要了
}
}
评价:堆排序是不稳定排序,堆执行一次调整需要
o(logn)时间,在排序过程中需要遍历所有元素执行堆调整,所以最终时间复杂度是o(nlogn)。
稳定排序与不稳定排序
相信大家都看到了,上面有一些排序是稳定排序,有一些是不稳定排序。那么它们有什么区别呢?
稳定排序与不稳定排序主要的区别在于对原序列中权值相等的元素的排序结果上。
对于权值相等的元素,稳定排序的结果依然会保证这些元素按照原序列中的排序不变。
对于权值相等的元素,在经过不稳定排序后,算法不保证这些元素仍按原序列中的顺序。
所以稳定排序主要的好处是:对于多个关键字的排序,我们可以使用稳定排序在上一次排序的基础上排序,使得第二次排序结果中关键字权重相等的那些项按照第一个关键字进行排序。
参考文献
- [1] http://yansu.org/2015/09/07/sort-algorithms.html
- [2] https://www.cnblogs.com/chengxiao
- [3] 维基百科