透镜畸变与相机标定

在相机成像的几何描述这篇文章中我们讨论了如何将一个点从世界坐标映射到像素坐标，不过那是比较理想的成像情况。现实世界中的相机在成像时还会受到透镜畸变的影响。

需要说明的是，下面的畸变模型都是基于针孔模型(一般的相机)得到的结果。而如果遇到一些特殊的相机，比如说鱼眼相机，它的投影模型会与针孔模型有些不同，它是投影在球面而不是平面上的。这样下面的畸变模型就不管用了。因此对于不同的相机，我们要使用不同的投影模型来建立畸变模型。

透镜畸变

现代相机为了获得更好的成像效果，相机里一般都加入了透镜。而透镜的加入对成像过程中光线的传播会产生新的影响，进而出现畸变，一般有两种主要的畸变（其实也还有其他的种类的畸变，但是不如这两种明显）：

径向畸变

• 径向畸变：透镜自身的形状对光线传播会有影响；
  • 桶形畸变：图像放大率随着与光轴之间的距离增加而减小
  • 枕形畸变：图像放大率随着与光轴之间的距离增大而增大

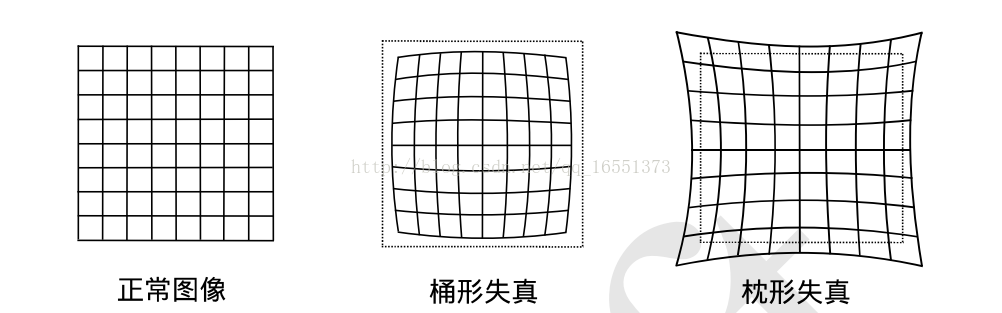
• 一般径向畸变对于二维平面上一个坐标(x,y)（如上图畸变最小的点为坐标原点，一般在图像中心，r是点到原点的距离）的影响可以使用如下公式表述：

\[ x_{distorted} = x( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6)　 \\ y_{distorted} = y( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6) \]

无论是桶形畸变还是枕形畸变，由于他们都是随着与中心之间的距离增加而增加，因此可以使用一个多项式函数来描述畸变前后的像素坐标变化。这个公式中，对于畸变较小的图像中心区域，畸变主要是\(k_1\)在起作用；而对于畸变较大的边缘区域，主要是\(k_2\)在起作用。一般的普通摄像头用这两个系数就已经可以很好地纠正径向畸变了。但是对于一部分畸变很大的摄像头，比如说鱼眼镜头等，还需要加入\(k_3\)畸变项才能比较好的表述畸变情况。

切向畸变

• 切向畸变：在机械组装过程中，透镜和成像平面不可能完全平行，这也会使得光线穿过透镜投影到成像面时的位置出现变化；

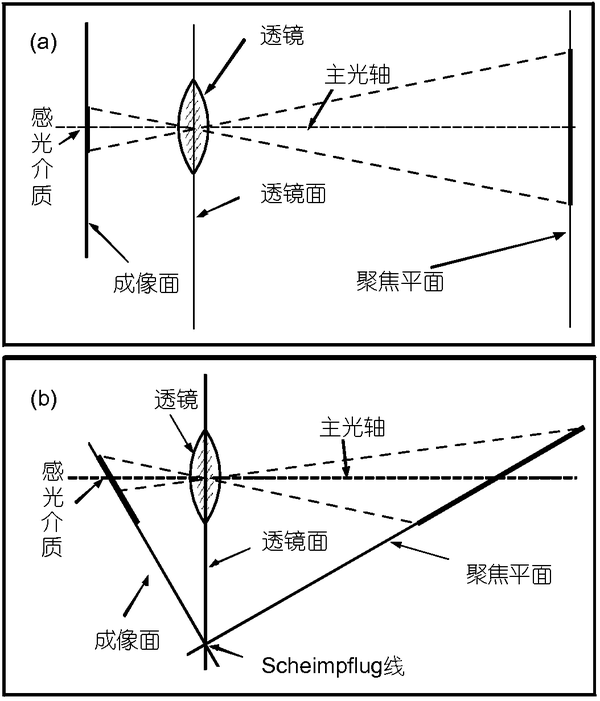
• 一般切向畸变对于二维平面上的坐标(x,y)的影响可以使用如下公式进行表述：

\[ x_{distorted} = x + [ 2p_1xy + p_2(r^2+2x^2)] \\ y_{distorted} = y + [ p_1(r^2+ 2y^2)+ 2p_2xy] \]

加入畸变的成像(理想情况下)

• 首先，世界坐标系下有一个固定的点P，世界坐标是 \(P_w\)

• 获得点P的相机坐标系坐标，可以利用相机外参R与t得到 \(P_c = RP_w + t\)

• 在2中获得的 \(P_c\) 仍然是三维的 (X,Y,Z) ，将其投影到归一化平面 \(Z=1\) 上，得到归一化相机坐标：\(P_C = [X/Z, Y/Z, 1]^T\)

• 此处加入畸变因素，畸变公式如下(其中，\(x=X/Z, y=Y/Z\))：

\[ x_{distorted} = x( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + [ 2p_1xy + p_2(r^2+2x^2)] \\ y_{distorted} = y( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + [ p_1(r^2+ 2y^2)+ 2p_2xy] \]

• 最后一步，利用内参K，将归一化相机坐标转换成像素坐标： \(P_{uv} = KP_{distorted}\)

\[ u = f_x x_{distorted} + c_x \\ v = f_y y_{distorted} + c_y \]

此处之所以将畸变放在内参前面作用，是因为上面已经说过了这个畸变模型假设的原点是图像中心，也就是未经过内参作用时符合。

相机标定

现在，我们知道，将一个三维世界坐标点通过相机映射到像素平面上一般需要三个矩阵参数，分别是相机外参、相机内参、畸变参数。而获得上述这些参数的过程便叫做相机标定。其中相机外参可以由相机的位姿固定获得，一般我们仅仅通过标定获得相机内参与畸变参数。而在某些时候，比如vio或rgbd-slam中，因为除了彩色相机外，也会有第二种传感器--imu或深度相机，此时为了后续的工作，我们也需要对两种传感器之间的外参进行精确标定。

需要说明的是相机标定只是对相机物理特性的近似获取。

对于相机的标定工作，已经有了很多的研究，主要可以分为两类：第一类是基于特定的实验条件，如形状、尺寸已知的标定物，利用一系列的数学变换与计算方法进行标定；第二类叫做自标定，不依赖于标定的参照物，仅仅利用摄像机在运动过程中周围环境的图像与图像之间的对应关系进行摄像机进行标定。

利用棋盘格的参数标定

1. 棋盘格可以提供很多三维世界中的路标点；
2. 相机采集后首先检测棋盘的角点；
3. 通过三维点与二维点的投影方程可以建立很多方程约束；
4. 通过非线性优化即可求出外参、内参、畸变参数；

对于一个具有N个格点的棋盘，假设我们拍摄K的角度的照片，则可以得到\(2NK\)个方程，如果我们想要求解出相机参数，则需要满足方程数量大于参数数量：（下面中K个角度有K组外参）

\[2NK >= 4 + 6K + 5 \]

此处需要说明的是，按照上述理解，只要一个棋盘上点足够多那不就一个视角就够了吗？这么做其实是不好的，因为在某个视角下，如果我们知道了其中一个格子的四个端点，那我们只需要继续延伸就可以得到其他的格点，那些多余的格点其实是不可以提供额外信息的，因次一个角度最好只利用四个点。这样上面的方程就可以变为

\[ 8K >= 4+6K+5 \]

即

\[ 2K >= 9 \]

理论上是这样，但是实际上当然是角度越多，可利用的路标点越多越好。

使用棋盘格标定彩色相机与深度相机的外参

1. 首先检测棋盘角点；
2. 明确一点：两个相机拍摄到的这些点在现实世界中是同一个点；
3. 利用深度相机的深度可以得到这些点在深度相机坐标系的三维坐标；
4. 假设一个外参R和T，便可以将这些点投影到彩色相机成像平面上；
5. 最小化重投影误差即可得到最合适的外参；

参考资料

• [1] 《视觉SLAM十四讲》，高翔著；
• [2] https://docs.opencv.org
• [3] 《学习OpenCV3》,O'REILLY著；