射影几何中的单应变换

各种经典变换总结(2维平面上，三维空间中思想一致，但是自由度不同)

1. 刚体(欧式)变换：可以保证两个点在变换前后欧式距离不变，具有3个自由度（旋转一个，平移两个）；
   • 通常是旋转加上平移；
2. 相似变换：通常指相似刚体变换，指增加了缩放的刚体变换，具有4个自由度（刚体的3个再加上缩放尺度），相似变换具有保角性与保持距离比的性质；
   • 通常可以描述为先旋转一次，再缩放一次，最后平移一次；
3. 仿射变换：具有两个旋转因子与两个缩放因子，外加两个平移因子，因此具有6个自由度（其实就是2*3矩阵每个元素都互不相关，都代表一个自由度），以前在理解齐次坐标中讲的仿射变换严格上来说是仿射变换的子集，甚至可以简单的使用相似变换达到。仿射变换不具有保角性与保持距离比的性质，但是原本的平行线，变换后仍然是平行线；
   • 通常可以描述为先旋转一个角度j1，然后在x方向缩放s1，y方向缩放s2，然后再反向旋转角度j，最后，再旋转一个角度j2，并平移一次；
4. 单应变换（也叫投影变换）：具有8个自由度，它的作用是描述两个平面上的点的映射关系。仿射变换的不变性对于投影变换不适用，但是原本共线的三个点在单应变换后仍旧共线。

三维空间中的变换

• 欧式变换: 6个自由度，长度、夹角、体积不变

\[ \begin{bmatrix} \mathbf{R} & \mathbf{t} \\ {\mathbf{0}^T} & 1 \end{bmatrix} \]

• 相似变换: 7个自由度， 体积比不变 \[ \begin{bmatrix} \mathbf{sR} & \mathbf{t} \\ {\mathbf{0}^T} & 1 \end{bmatrix} \]

• 仿射变换: 12个自由度，平行性、体积比不变 \[ \begin{bmatrix} \mathbf{A} & \mathbf{t} \\ {\mathbf{0}^T} & 1 \end{bmatrix} \]

• 射影变换: 15个自由度，接触平面的相交与相切不变 \[ \begin{bmatrix} \mathbf{A} & \mathbf{t} \\ {\mathbf{a}^T} & \mathbf{v} \end{bmatrix} \]

单应变换

如下面公式，实际上单应变换实现的是两个平面之间的映射关系。(意思是只要是从一个平面到另一个平面的映射都可以用单应矩阵表示)

\[ s \begin{bmatrix} x^{'} \\ y^{'} \\ 1 \end{bmatrix} = H \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \]

单应矩阵的维度是3*3，却只有8个自由度，这是因为齐次坐标的尺度等价性。一般求出的单应矩阵会进行归一化，要求为\(h_{33} = 1\)或\(h_{11}^2 + h_{12}^2 + h_{13}^2 + h_{21}^2 + h_{22}^2 + h_{23}^2 + h_{31}^2 + h_{32}^2 + h_{33}^2 = 1\)

同理，在理解对极几何与基本矩阵中我们有得出结论，本质矩阵\(E = t^{\land} R\)，由于平移与旋转共有6个自由度。但是由于其次坐标的的尺度等价性，本质矩阵实际上有5个自由度。

单应变换的作用

1. 相机位姿的估计
2. 图像的矫正
3. 全景拼接

使用单应变换进行相机位姿估计

jihe

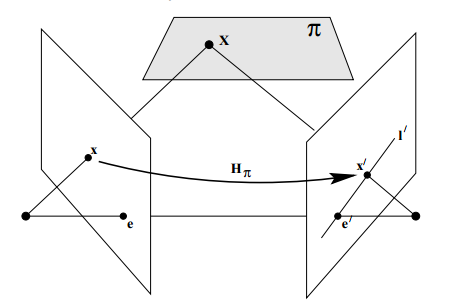
这个功能与使用基础矩阵对相机的位姿进行估计是类似的。首先：

\[ Z_1p_{uv1} = KP_w \\ Z_2p_{uv2} = K(RP_w + t) 　\tag{1}\]

其中K是相机内参，R与t是相机的位姿变换，\(P_w\)是一个空间点在第一个相机坐标系下的坐标。Z是空间点到相机光心的距离，\(p_{uv}\)是空间点在两个位置的相机的像素平面上的像素坐标。

我们假设有一个参照物平面，平面方程如下：

\[ n^{T} P_w + d = 0 　\tag{2} \]

稍加整理可得：

\[ -\frac{n^{T}P_w}{d} = 1 \tag{3} \]

所以，由公式1我们可以得到：

\[ \begin{equation} \begin{split} p_{uv2} &= K(RP_w + t)/Z_2 \\ &= K(RP_w + t \cdot -\frac{n^{T}P_w}{d})/Z_2 \\ &= K(R + t \cdot -\frac{n^{T}}{d})P_w/Z_2 \\ &= K(R + t \cdot -\frac{n^{T}}{d}) K^{-1}p_{uv1} \end{split} \end{equation} \]

如上，上述得到了第一个相机平面上的点到第二个相机平面上的点的映射变换，这部分可以使用下式表示(s是一个齐次坐标的归一系数，为了数学等式的成立)：

\[ sp_{uv2} = Hp_{uv1} \\ H = K(R + t \cdot -\frac{n^{T}}{d}) K^{-1} \]

我们发现这个单应矩阵H的定义与旋转、平移、还有平面的参数有关。

单应约束与対极约束的区别

• 対极约束：基础矩阵描述的本质是一种点到直线的映射关系，所以対极约束不能给出两幅图像上的点的一一对应关系，只能给出点对应的必要条件。但是，対极约束与场景的结构无关，只与相机的参数有关。

• 单应约束：单应矩阵描述的本质是点到点的映射关系，所以单应约束给出了两幅图像上的点的一一对应关系，这是一种充要的条件。但是，单应约束需要做这些投影的空间点本身在一个平面上（即深度本身满足一定要求）,否则使用单应矩阵进行的映射结果会出现错误。如下图p'点不在平面P上，所以使用对应的单应矩阵做投影会得到错误的投影点\(x_2\)，，正确的应该是\({x_2}^{'}\)。

homography

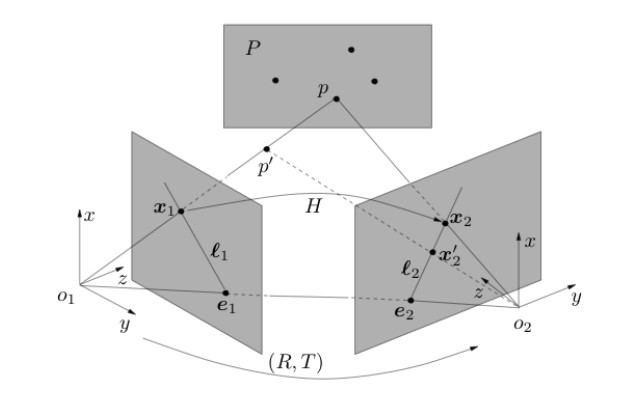
• 在只有旋转没有平移时，対极约束是恒成立的，此时不能用本质矩阵进行相机的位姿估计。而单应矩阵可以。

• 推导中我们使用了齐次坐标，所以单应约束也是尺度无关的，恢复出来的位姿变化也具有尺度不确定性。

使用单应变换进行透视矫正

使用单应变换进行全景拼接

参考资料

• [1] https://docs.opencv.org/3.4.1/d9/dab/tutorial_homography.html
• [2] Richard Hartley and Andrew Zisserman. Multiple view geometry in computer vision. Cambridge university press, 2003.
• [3] 《学习opencv3》