相机成像的几何描述
相机成像,就是指通过摄像机将真实的三维空间中的点映射到成像平面(2维)上。这个过程可以通过一个几何模型来表示,本文使用最简单的针孔成像模型进行讲解。
针孔相机模型
如下图所示,是针孔相机的成像模型。
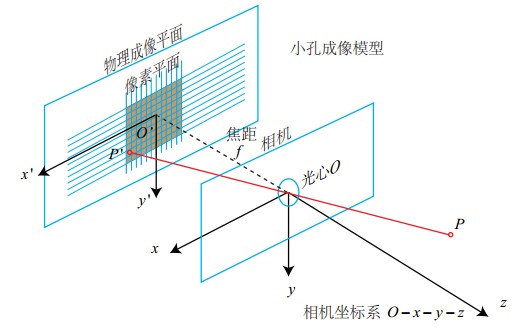
其中,O为相机的光心,也是针孔模型的针孔。现实世界的空间点P,在经过小孔O投影之后,落在了物理成像平面O'-x'-y'上,成像点是
P' ,假设P的相机坐标系坐标是\([X,Y,Z]^T\),P' 的相机坐标系坐标为\([X',Y',Z']^T\),并且假设物理成像平面到小孔的距离为f(焦距)。则这会构成如下相似三角形
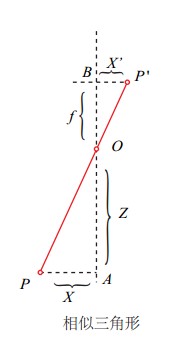
那么根据三角形相似的关系有:
\[\frac{Z}{f} = - \frac{X}{X'} = - \frac{Y}{Y'}\]
其中负号是因为成的像是倒的,所以坐标系数会相反,不过一般为了简化模型,我们统一将成像平面对称到相机的前方,使得成像平面与三维空间点一起放在摄像机坐标系的同一侧,这叫做虚像。这样,我们可以去掉上式中的负号,如下:
\[\frac{Z}{f} = \frac{X}{X'} = \frac{Y}{Y'}\]
此处之所以可以随意的将成像平面挪到前方,是因为我们拍照相机输出的照片都是正常的,并不是倒像,这是因为相机自身的软件会帮助我们翻转这张图片。虽然原理上小孔成像是倒的,但是实际应用中我们在理解照片与实际场景的成像时应该是将成像平面放到前面的。
相机几何坐标转换
如上的针孔模型,一个空间点在投影到2d的像素平面上时会经历如下三步: 1. 空间点从世界坐标系转换到相机坐标系; 2. 由空间点的相机坐标系的坐标得到成像平面上投影点的坐标; 3. 最后由成像平面投影点的坐标得到像素平面上的像素坐标。

从世界坐标系到相机坐标系
这个转换很容易完成,是一种刚体运动,可以用平移、旋转来描述 - 第一步是平移操作,平移操作变换是将光心位置移动到坐标原点的那个向量。 - 第二步是旋转操作,旋转矩阵是将相机角度旋转到朝向z轴的那个矩阵。
\[ P_c=R(P_w - C) \]
上式中,R是旋转矩阵,C是一个平移矩阵,式中将其写为了负的形式,整个矩阵形式如下图

此处的旋转与平移信息相对于相机的一些内部参数而言属于外部参数,在讨论相机外部参数时,往往会将上式写成如下形式,使用R与T的联合矩阵(4*4)来表示相机外参(一般是对相机位姿求逆)
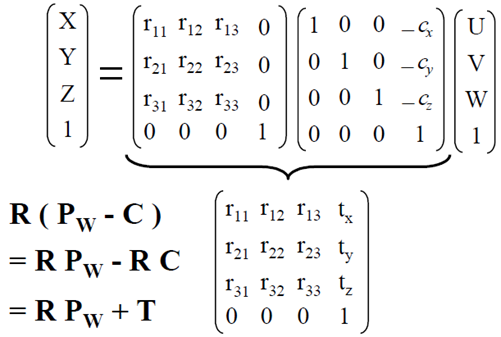
由空间点的相机坐标系的坐标得到成像平面上投影点的坐标
这部分变换其实前面已经讲过了,成像平面与真实物体还有相机光心的位置大概如下所示(下图中我们使用新的坐标命名参数):
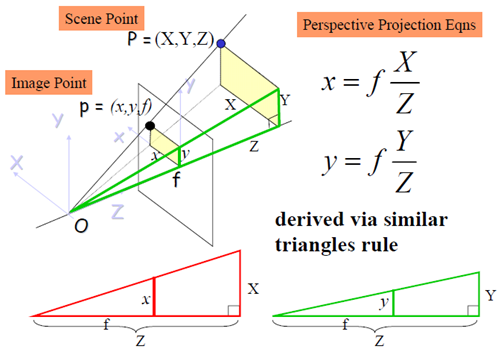
其中相机坐标系坐标(X,Y,Z)到投影平面上的齐次坐标(x,y,1)可以表示如上。
注意,此处主要是两步,第一步是\((X,Y,Z)\)变为\((\dfrac{X}{Z}, \dfrac{Y}{Z}, 1)\),即从相机坐标系坐标变换到归一化平面上。第二步是将\((\dfrac{X}{Z}, \dfrac{Y}{Z})\)变换为\((f \dfrac{X}{Z}, f \dfrac{Y}{Z})\),即将坐标从归一化平面变换到成像平面上。这里的第二步其实是包含在了内参操作里的。
转换为像素坐标
由上已经知道,空间点相机坐标系坐标(X,Y,Z)到成像平面投影的坐标(x,y)变换为
\[ x = f\frac{X}{Z} \]
\[ y = f\frac{Y}{Z} \]
而像素坐标系通常的定义方式是:原点o'位于图像的左上角,\(\mu\)轴向右与本来x轴平行,\(\nu\)轴向下与y轴平行。像素坐标系与成像平面之间,相差了一个缩放和一个原点的平移。我们假设像素坐标在\(\mu\)轴上缩放了\(\alpha\)倍,在\(\nu\)上缩放了\(\beta\)倍。同时,原点平移了\([c_x,c_y]^T\)。所以,(x,y)与(u,v)的关系如下:
\[ u = \alpha x + c_x \]
\[ v = \beta y + c_y \]
其中\(\alpha\)代表的含义可以理解为横轴分辨率(1m有多少像素),\(\beta\)类似,接下来将上面两个式子合并,得到直接从相机坐标系坐标到像素坐标的变换如下:
\[ u = f_x\frac{X}{Z} + c_x \]
\[ v = f_y\frac{Y}{Z} + c_y \]
其中,将\(\alpha f\)合并成\(f_x\),\(\beta f\)合并成\(f_y\)。
下面是使用矩阵表示,左边使用齐次坐标。
\[ \left( \begin{array}{ccc} u\\ v\\ 1 \end{array} \right) = \frac{1}{Z} \left( \begin{array}{ccc} f_x& 0 & c_x\\ 0& f_y& c_y\\ 0 & 0& 1 \end{array} \right) \left( \begin{array}{ccc} X\\ Y\\ Z \end{array} \right) = \frac{1}{Z} K P_c \]
其中矩阵K就是相机的内参矩阵,我们通常认为,内参矩阵在相机出厂之后是固定的,不会再使用过程中发生变化。有时我们并不知道相机的内参,自己确定内参的操作叫做标定。
还有一点可以观察到,在相机坐标系下,从原点出发的射线上的点全部都投影到一个像素坐标上了。这个可以通过将上式右边的三维坐标
(X,Y,Z)任意乘以一个常数,由于齐次坐标的尺度等价性,最后的投影结果不会改变。
总结:公式变换过程
换一种方式更详细地进行总结(此处有简化细节): 1. 首先,世界坐标系下有一个固定的点P,世界坐标是 \(P_w\)
获得点P的相机坐标系坐标,可以利用相机外参R与t得到 \(P_c = RP_w + t\)
在2中获得的 \(P_c\) 仍然是三维的 (X,Y,Z) ,将其投影到归一化平面 \(Z=1\) 上,得到归一化相机坐标:\(P_C = [X/Z, Y/Z, 1]^T\)
最后一步,利用内参K,将归一化相机坐标转换成像素坐标: \(P_{uv} = KP_C\)
上述整合起来也得到:
\[ ZP_{uv} = K(RP_w + t) \]
参考上面详细的成像原理,其实总结中的第三步与第四步是可以没有先后关系的。因为都是线性的运算,所以谁先谁后都不影响最后结果。
参考资料
- [1] 《视觉SLAM十四讲》,高翔著;
- [2] http://www.cnblogs.com/gemstone/archive/2011/12/19/2293932.html