线性判别分析(LDA)
线性判别分析(Linear Discriminant Analysis,简称LDA)是一种经典的有监督线性学习方法,最早在1936年由fisher在二分类问题上提出。这种方法主要用于分类与降维。此处需要说明的是,LDA常常还会是隐含狄利克雷分布(Latent Dirichlet Allocation)的简称,这是自然语言处理领域一种处理文档的主题模型,与本文讲的线性判别分析关系不大。
基本思想
LDA的思想及其朴素,这是一种有监督学习的技术。给定训练样例集合,设法将样例投影到低维度的空间里,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离。概括一下为投影后类内方差最小,类间方差最大。 > 一般广义线性模型可表示为\(y = g^{-1}(W^{T}x)\),其中W完成线性映射,g函数为联系函数,可以完成非线性转换(比如分类时将回归连续值转换成离散值)。LDA要做的其实是首先使用W将样本从高维空间映射到低维空间,然后根据y的真值将样本分成一群群,通过最大化样本的类间距离、最小化样本的类内方差原则来估计出W。
为了尽量表达清楚,先从最简单的二分类的LDA进行讲解。如下图:
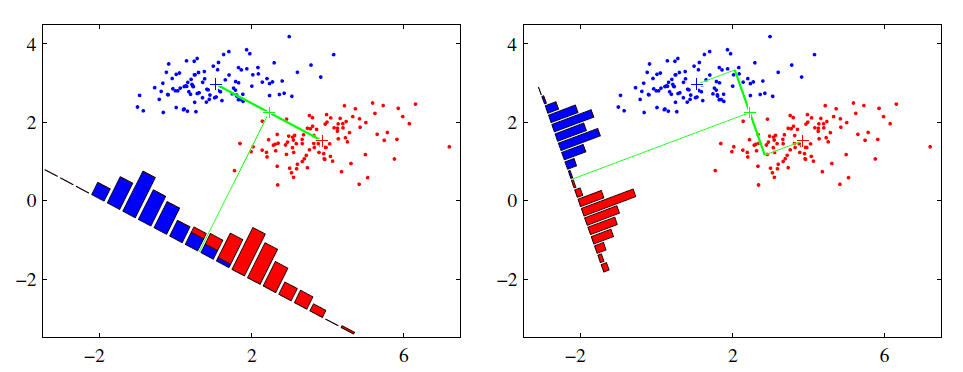
二分类LDA
假设有数据集\(D=\{(x_1,y_1), (x_2,y_2), ...,((x_m,y_m))\}\),其中\(x_i\)为n维向量,\(y_i \in \{0,1\}\)。我们定义
- \(N_j(j=0,1)\)为第j类样本的个数;
- \(X_j(j=0,1)\)为第j类样本的集合;
- \(u_j(j=0,1)\)为第j类样本的均值向量,即\(\mu_j = \frac{1}{N_j}\sum\limits_{x \in X_j}x\;\;(j=0,1)\);
- \(\Sigma_j(j=0,1)\)为第j类样本的协方差矩阵,即\(\Sigma_j = \sum\limits_{x \in X_j}(x-\mu_j)(x-\mu_j)^T\;\;(j=0,1)\);
由于两类,所以只需要将数据投影到一条直线上即可。投影到一条直线上,则:
- 投影矩阵是一个向量,假设为w
- 样本\(x_i\)投影后为\(w^Tx_i\)
- 投影后的样本中心为\(w^Tu_i\)
- 投影后类间方差为\(w^T\Sigma_0w\)与\(w^T\Sigma_1w\),类内方差为
\[ ||w^T\mu_0-w^T\mu_1||_2^2 = w^T(\mu_0-\mu_1)(\mu_0-\mu_1)^Tw \]
我们的目标是投影后类内方差最小,类间方差最大,即:
\[ \underbrace{arg\;max}_w\;\;J(w) = \frac{||w^T\mu_0-w^T\mu_1||_2^2}{w^T\Sigma_0w+w^T\Sigma_1w} = \frac{w^T(\mu_0-\mu_1)(\mu_0-\mu_1)^Tw}{w^T(\Sigma_0+\Sigma_1)w} \]
一般我们定义类内散度为\(S_w\)为:
\[ S_w = \Sigma_0 + \Sigma_1 = \sum\limits_{x \in X_0}(x-\mu_0)(x-\mu_0)^T + \sum\limits_{x \in X_1}(x-\mu_1)(x-\mu_1)^T \]
类间散度为\(S_b\)为:
\[ S_b = (\mu_0-\mu_1)(\mu_0-\mu_1)^T \]
最后,我们将优化目标重写为
\[ \underbrace{arg\;max}_w\;\;J(w) = \frac{w^TS_bw}{w^TS_ww} \]
最后的这个优化结果其实是一个广义瑞利商
瑞利商与广义瑞利商
瑞利商
瑞利商是指这样的函数\(R(A,x)\)
\[ R(A,x) = \frac{x^HAx}{x^Hx} \]
其中: - x为非零向量 -
A为n*n的Hermitan矩阵(共轭转置等于自身的矩阵),即\(A^H = A\),只要A为实矩阵,并且满足\(A^T=A\),即为一个Hermitan矩阵。
瑞利商\(R(A,x)\)有一个非常重要的性质,即它的最大值等于矩阵A最大的特征值(此时x为对应的特征向量),而最小值等于矩阵A的最小的特征值,也就满足
\[ \lambda_{min} \leq \frac{x^HAx}{x^Hx} \leq \lambda_{max} \]
我们可以发现瑞利商的分子分母都是x的二次项,所以最后的结果肯定是与x的长度无关的,只会与x的方向有关,这个结论刚好体现了这样一点。
广义瑞利商
广义瑞利商是指这样的函数\(R(A,B,x)\);
\[ R(A,x) = \frac{x^HAx}{x^HBx} \]
其中: - x为非零向量 -
而A,B为n*n的Hermitan矩阵。B为正定矩阵。
另\(x = B^{-1/2}x'\),此处分母可以转换成:
\[ x^HBx = x'^H(B^{-1/2})^HBB^{-1/2}x' = x'^HB^{-1/2}BB^{-1/2}x' = x'^Hx' \]
分子可以转换成:
\[ x^HAx = x'^HB^{-1/2}AB^{-1/2}x' \]
此时我们的\(R(A,B,x)\)转化为 \(R(A,B,x')\)
\[ R(A,B,x') = \frac{x'^HB^{-1/2}AB^{-1/2}x'}{x'^Hx'} \]
利用前面的瑞利商的性质,我们可以很快的知道,\(R(A,B,x)\)的最大值为矩阵\(B^{-1/2}AB^{-1/2}\)的最大特征值,而最小值为矩阵\(B^{-1/2}AB^{-1/2}\)的最小特征值。或者说是\(B^{-1}A\)的最大特征值。
二类LDA的广义瑞利商结果
接下来回到二类LDA的优化目标
\[ \underbrace{arg\;max}_w\;\;J(w) = \frac{w^TS_bw}{w^TS_ww} \]
这个广义瑞利商的最大值为矩阵\(S^{−\frac{1}{2}}_wS_bS^{−\frac{1}{2}}_w\)的最大特征值,对应的w为其对应的特征向量。而\(S_w^{-1}S_b\)的特征值和\(S^{−\frac{1}{2}}_wS_bS^{−\frac{1}{2}}_w\)的特征值相同,\(S_w^{-1}S_b\)的特征向量w'和\(S^{−\frac{1}{2}}_wS_bS^{−\frac{1}{2}}_w\)的特征向量满足\(w' = S^{−\frac{1}{2}}_ww\)的关系。 ## 多类LDA - 数据集\(D=\{(x_1,y_1), (x_2,y_2), ...,((x_m,y_m))\}\),其中\(x_i\)为n维向量,\(y_i \in \{C_1,C_2,...,C_k\}\)为所属类别 - 我们定义\(N_i\)为第i类样本个数,\(X_i\)为第i类样本的集合 - \(\mu_i\)为第i类样本的均值向量,\(\Sigma_i\)为第i类样本的协方差矩阵。
此时为多类向低维度空间的投影,我们假设投影到的低维度空间的维度为d,对应的基向量为\((w_1,w_2,...w_d)\),基向量组成的投影矩阵为W,它是一个n*d的矩阵(d==1为二分类情况)。
此时优化目标是:
\[ \frac{W^TS_bW}{W^TS_wW} \]
其中, - \(S_b = \sum\limits_{j=1}^{k}N_j(\mu_j-\mu)(\mu_j-\mu)^T\),代表类间散度(u为所有样本均值向量) - \(S_w = \sum\limits_{j=1}^{k}S_{wj} = \sum\limits_{j=1}^{k}\sum\limits_{x \in X_j}(x-\mu_j)(x-\mu_j)^T\),代表类内散度之和
此时,\(W^TS_bW\)与\(W^TS_wW\)都是矩阵,不是标量,无法作为一个标量函数进行优化。
可以将上式进行分解(与奇异值分解压缩形式类似)
\[ J(W) = \frac{W^TS_bW}{W^TS_wW} = \frac{\prod\limits_{i=1}^dw_i^TS_bw_i}{\prod\limits_{i=1}^dw_i^TS_ww_i} = \prod\limits_{i=1}^d\frac{w_i^TS_bw_i}{w_i^TS_ww_i} \]
此时右边又变成了广义瑞利商。每个乘积项最大值是矩阵\(S_w^{-1}S_b\)的最大特征值,最大的乘积就是矩阵\(S_w^{-1}S_b\)的最大的d个特征值的乘积。此时对应的投影矩阵W就对应着最大的d个特征值对应的特征向量张成的矩阵。
LDA算法流程
- 输入:数据集\(D=\{(x_1,y_1), (x_2,y_2), ...,((x_m,y_m))\}\),其中任意样本\(x_i\)为n维向量,\(y_i \in \{C_1,C_2,...,C_k\}\),降维到的维度d。
- 输出:投影矩阵W与降维后的样本集D'
- 计算类内散度矩阵\(S_w\)
- 计算类间散度矩阵\(S_b\)
- 计算矩阵\(S_w^{-1}S_b\)
- 计算\(S_w^{-1}S_b\)最大的d个特征值和对应的d个特征向量\((w_1,w_2,...w_d)\),得到投影矩阵W(二分类时是向量)
- 对样本集中的每一个样本特征\(x_i\),转化成新的样本\(z_i = W^Tx_i\);
- 得到输出样本集\(D'=\{(z_1,y_1), (z_2,y_2), ...,((z_m,y_m))\}\)
LDA与PCA的比较
- 这两种方法都有降维的思想
- pca是无监督的,lda是有监督的
- pca主要用来压缩与简化
- lda是一种线性分类器,主要用来分类等
参考资料
- [1] 《机器学习》,周志华著;
- [2] https://www.cnblogs.com/pinard/p/6244265.html