矩阵的奇异值分解(SVD)
矩阵的本质可以是代表着一定维度空间上的线性变换。矩阵分解的本质是将原本m*n复杂的矩阵分解成对应的几个简单矩阵的乘积的形式。使得矩阵分析起来更加简单。
前面写过一篇博客讲的是矩阵的特征值分解,但是我们知道很多矩阵都是不能够进行特征值分解的。这种情况下,如果我们想通过矩阵分解的形式将原本比较复杂的矩阵问题分解成比较简单的矩阵相乘的形式,会对其进行奇异值分解。
简单回顾特征值分解
如果一个n*n矩阵A有n个特征值,并且这n个特征值所对应的n个特征向量线性无关,则矩阵A可以使用下式进行特征值分解:
\[ A=W\Sigma W^{-1} \]
其中,W是n个特征向量所张成的n*n维矩阵,而\(Sigma\)是一个对角矩阵,对角线上是矩阵A的n个特征值。
一般情况下,我们会将特征向量标准化(即令他们是单位向量),此时矩阵W的n个特征向量为标准正交基,所以会有\(W^TW=I\),即\(W^T=W^{-1}\),也就是说W为酉矩阵。所以特征值分解也可以写成\(A=W\Sigma W^T\)
奇异值分解
奇异值分解并没有特征值分解那么苛刻的要求,对于任意一个m*n的矩阵A,可以对其进行如下奇异值分解:
\[ A = U\Sigma V^T \]
其中, - U是一个m*m的矩阵; - \(Sigma\)是一个m*n的对角矩阵,主对角线上的元素成为奇异值;
-
V是一个n*n的矩阵,U与V都是酉矩阵,即组成它们的都是标准正交基。
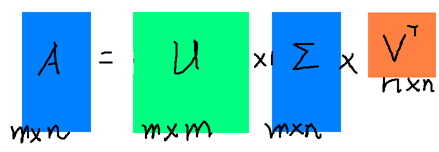
如何奇异值分解?
首先,利用A的转置乘以A会得到一个
n*n的矩阵\(A^TA\),对这个矩阵进行特征值分解,得到的n个特征向量张成的n*n矩阵就是V矩阵,在这里我们将V中的每一个特征向量叫做A的右奇异向量;然后,利用A乘以A的转置得到
m*m的矩阵\(AA^T\),对这个矩阵进行特征值分解,得到的m个特征向量张成的m*m矩阵就是U矩阵,在这里我们将每一个特征向量叫做左奇异向量;最后,利用下式求得每个奇异值 \[A=U\Sigma V^T \Rightarrow AV=U\Sigma V^TV \Rightarrow AV=U\Sigma \Rightarrow Av_i = \sigma_i u_i \Rightarrow \sigma_i = Av_i / u_i\]
上述奇异值分解步骤的依据
在上面,我们说矩阵\(A^TA\)的特征向量组成的就是SVD的V矩阵,矩阵\(AA^T\)的特征向量组成的就是SVD的U矩阵,可以通过如下推导证明(以V矩阵为例):
\[ A=U\Sigma V^T \Rightarrow A^T=V\Sigma^T U^T \Rightarrow A^TA = V\Sigma^T U^TU\Sigma V^T = V\Sigma^2V^T \]
上式中我们还发现矩阵\(A^TA\)特征值矩阵等于A奇异值矩阵的平方,即\(\sigma_i = \sqrt{\lambda_i}\),所以其实在第三步中我们求奇异值的方式其实也可以通过求出矩阵\(A^TA\)的特征值取平方根来求奇异值。
SVD求解实例
- 对于一个矩阵A:
\[ \mathbf{A} = \left( \begin{array}{ccc} 0& 1\\ 1& 1\\ 1& 0 \end{array} \right) \]
- 首先计算出\(A^TA\)和\(AA^T\)
\[ \mathbf{A^TA} = \left( \begin{array}{ccc} 0& 1 &1\\ 1&1& 0 \end{array} \right) \left( \begin{array}{ccc} 0& 1\\ 1& 1\\ 1& 0 \end{array} \right) = \left( \begin{array}{ccc} 2& 1 \\ 1& 2 \end{array} \right) \]
\[ \mathbf{AA^T} = \left( \begin{array}{ccc} 0& 1\\ 1& 1\\ 1& 0 \end{array} \right) \left( \begin{array}{ccc} 0& 1 &1\\ 1&1& 0 \end{array} \right) = \left( \begin{array}{ccc} 1& 1 & 0\\ 1& 2 & 1\\ 0& 1& 1 \end{array} \right) \]
- 求出\(A^TA\)的特征值与特征向量
\[ \lambda_1= 3; v_1 = \left( \begin{array}{ccc} 1/\sqrt{2} \\ 1/\sqrt{2} \end{array} \right); \lambda_2= 1; v_2 = \left( \begin{array}{ccc} -1/\sqrt{2} \\ 1/\sqrt{2} \end{array} \right) \]
- 求出\(AA^T\)的特征值与特征向量
\[ \lambda_1= 3; u_1 = \left( \begin{array}{ccc} 1/\sqrt{6} \\ 2/\sqrt{6} \\ 1/\sqrt{6} \end{array} \right); \lambda_2= 1; u_2 = \left( \begin{array}{ccc} 1/\sqrt{2} \\ 0 \\ -1/\sqrt{2} \end{array} \right); \lambda_3= 0; u_3 = \left( \begin{array}{ccc} 1/\sqrt{3} \\ -1/\sqrt{3} \\ 1/\sqrt{3} \end{array} \right) \]
- 利用\(Av_i = \sigma_i u_i, i=1,2\)求得奇异值,我们会发现求得的结果与$ _i = $的结果相同;
\[ \left( \begin{array}{ccc} 0& 1\\ 1& 1\\ 1& 0 \end{array} \right) \left( \begin{array}{ccc} 1/\sqrt{2} \\ 1/\sqrt{2} \end{array} \right) = \sigma_1 \left( \begin{array}{ccc} 1/\sqrt{6} \\ 2/\sqrt{6} \\ 1/\sqrt{6} \end{array} \right) \Rightarrow \sigma_1=\sqrt{3} \]
\[ \left( \begin{array}{ccc} 0& 1\\ 1& 1\\ 1& 0 \end{array} \right) \left( \begin{array}{ccc} -1/\sqrt{2} \\ 1/\sqrt{2} \end{array} \right) = \sigma_2 \left( \begin{array}{ccc} 1/\sqrt{2} \\ 0 \\ -1/\sqrt{2} \end{array} \right) \Rightarrow \sigma_2=1 \]
- 最终得到A的奇异值分解为
\[ A=U\Sigma V^T = \left( \begin{array}{ccc} 1/\sqrt{6} & 1/\sqrt{2} & 1/\sqrt{3} \\ 2/\sqrt{6} & 0 & -1/\sqrt{3}\\ 1/\sqrt{6} & -1/\sqrt{2} & 1/\sqrt{3} \end{array} \right) \left( \begin{array}{ccc} \sqrt{3} & 0 \\ 0 & 1\\ 0 & 0 \end{array} \right) \left( \begin{array}{ccc} 1/\sqrt{2} & 1/\sqrt{2} \\ -1/\sqrt{2} & 1/\sqrt{2} \end{array} \right) \]
奇异值分解用于压缩
- 首先,对于奇异值分解\(A = U\Sigma V^T\),我们也可以写成如下形式,我们假设奇异值大小顺序排列,即\(\sigma_1 \geq \sigma_2 \geq...\geq \sigma_n>0\),并且其中每一项的\(uv^T\)都是秩为1的(m*n)矩阵。
\[ A = \sigma_1u_1v_1^T + \sigma_2u_2v_2^T + ... + \sigma_nu_nv_n^T \]
- 对于如下一幅图像,像素(矩阵尺度)为
450*333

- 我们如果只保留最大的奇异值那一项,即另\(A_1 = \sigma_1u_1v_1^T\),然后保存这个矩阵,图像显示如下:

- 保留前五项,得到下图:

- 保留前50项,得到下图:

我们会发现保留前50项就已经得到很不错的图像了,但是这时需要存储的元素为
(1+450+333)*50=39200个,远远小于450*333=149850个。
奇异值分解与特征值分解的思考
这两种分解都是在矩阵分析中对复杂矩阵进行简化矩阵的手段;
奇异值全都大于0,因为是平方根,所以肯定大于0
如果将矩阵看做是线性变换的话,特征值分解与奇异值分解都是将矩阵分解成三个线性变换的叠加(两个旋转,一个拉伸)
特征值分解与奇异值分解都可以用于压缩矩阵(通过抛弃较小的奇异值/特征值),pca降维时的计算方式就与其很相关。
在opencv中提供了
cv::SVD可以直接对矩阵进行奇异值分解
参考资料
- [1] 《学习opencv3》(中文版)
- [2] https://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html
- [3] https://www.cnblogs.com/pinard/p/6251584.html
- [4] https://www.zhihu.com/question/22237507