主成分分析(PCA)

1. 主成分分析原理介绍

PCA是一种无监督的降维方法，主要作用是压缩与简化

顾名思义，主成分分析(PCA)是用来分析数据的主要成分的。

打个比方，一些ｎ维点可以用一个ｎ维的坐标完全表示。主成分分析，可以提取出ｎ个空间基向量来表示这些数据点。不过你可以理解成这ｎ个空间基向量是按顺序求出的，首先根据这些ｎ维点确定第一个空间基向量方向，使得如果只能用一个基向量来表示这些点，只使用这个基向量表示这些二维点误差最小。然后求下一个基向量，使得只使用这两个基向量表示这些ｎ维点误差最小。依次类推，直到求出n维度完备的空间向量基，便肯定可以完全表示了。

pca_line

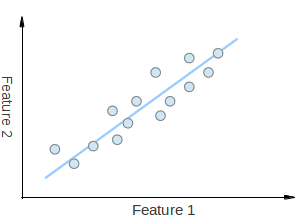
如上图，是根据一些二维点计算出来的第一个“主成分”基向量。

pca_eigen

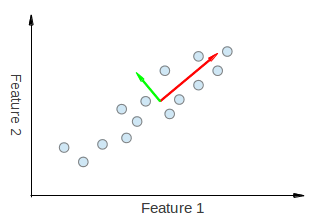
如上图，是这些二维点的两个主成分基向量。

由上面分析我们发现，PCA可以用来做降维。虽然肯定会有些精度损失，但是这已经是最小的精度损失了。

2. 主成分分析(PCA)的代码实现

通常m个n维点排列在一起会得到一个m*n矩阵，很奇妙的是，我们可以通过数学推导得出ｎ个特征向量，这个矩阵包含的点集合的主成分就是这n个特征向量集合。这些特征向量的代表的主要成分的重要重要程度可以用其对应的特征值来衡量，特征值越大，其对应的特征向量代表的主成分越重要。

比如你有\(x_1...x_m\)总共m个数据，其中每个数据由n个变量表示，我们的目的是将这m个数据使用少于n个变量表示，比如将维度降为p，p<n。这个过程叫做降维。具体操作步骤如下： ## 2.1 组织数据集 首先将数据整理成如下固定形式。 - 将\(x_1...x_m\)写成行向量，每一行有n个元素，即n列。 - 将这些行向量放入一个单一的矩阵x，矩阵维度是m*n

2.2 计算经验均值

• 计算每一个维度的经验均值，维度总共有\(j = 1, ..., n\)
• 将计算出来的n个经验均值放入一个向量u，这个向量维度是n*1

\[ \mathbf{u[j]} = \frac{1}{m}\sum_{i=1}^{m}\mathbf{X[i,j]} \]

2.3 计算离均值的偏差矩阵

我们计算均值的原因是我们想把数据搬移到原点附近，让原点处于这些数据的中心，这样可以使得均方误差最小。所以这一步要做的就是： - 将矩阵x的每一行都减去均值向量u - 得到一个新的均值矩阵B，维度也是m*n

上述操作可以使用如下方式完成

\[ \mathbf{B} = \mathbf{X} - \mathbf{h}\mathbf{u^{T}} \]

其中，h是一个m*1的列向量，并且值为全1。

2.4 计算上述偏差矩阵的协方差矩阵

• 这一步是计算B矩阵的协方差矩阵C，C矩阵的维度会是n*n。可以使用下式实现

\[ \mathbf{C} = \frac{1}{m-1} \mathbf{B^{*}} \cdot \mathbf{B} \]

上式中*是共轭转置运算符。不过由于一般B中包含的都是实数，所以在大部分情况下这个操作相当于一个转置运算符。

2.5 由特征值分解求得上一步中协方差矩阵的特征值与特征向量

首先说明一下，特征值与特征向量还有矩阵之间的关系。

特征向量是矩阵空间的基向量，长度为1，特征向量之间互相正交，特征值是矩阵在对应特征向量上的投影。将矩阵理解成一种变换，则每个特征向量就是这个变换的一个方向，对应的特征值就是在这个方向上的变换速度。

一般对于一个矩阵C(维度为n*n)，会存在n个特征向量(每个维度都是n)，与n个特征值，每个特征值对应一个特征向量。它们之间的关系如下：

\[ \mathbf{V^{-1}} \mathbf{C} \mathbf{V} = \mathbf{D} \] 也可以写成　 \[ \mathbf{C} = \mathbf{V} \mathbf{D} \mathbf{V^{-1}} \]

其中， - V是n个特征向量组成的n*n维矩阵 - D是n个特征值组成的一个对角矩阵（只有对角线上值不为0，维度也是n*n） - 上面V与D中的特征向量与特征值是有序配对的，即第i个特征值对应第i个特征向量

特征值分解(变换矩阵必须是方阵)就是从矩阵C中分解出V与D，我们下面可以做的就是根据特征值的大小保留前p个特征向量，作为新的维度基础。实现将n维度降维到p维度。

3. opencv中的cv::PCA类的使用

见我的github

4. 参考资料

• [1] https://docs.opencv.org/3.4.1/d1/dee/tutorial_introduction_to_pca.html
• [2] https://robospace.wordpress.com/2013/10/09/object-orientation-principal-component-analysis-opencv/
• [3] https://en.wikipedia.org/wiki/Principal_component_analysis