图像特征之Harris角点检测
1. 角点与角点的检测
1.1 什么是角点?
从图像分析的角度来看,一般而言角点有如下两种定义: 1. 角点可以是两个边缘的角点; 2. 角点是邻域内具有两个主方向的特征点;
如同下图所示,前俩例子一个是平坦区域,一个是边缘。第三个就如上述两种定义方式的角点一样,设置一个滑动窗口,无论朝那个方向移动,对应位置上的亮度都会有很大变化,
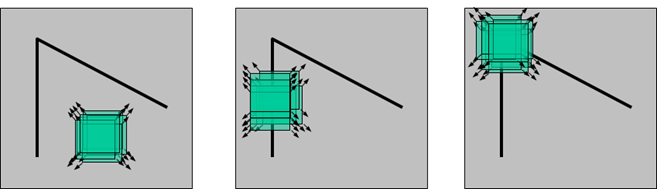
1.2 不同的角点检测方法
角点定义出来了以后,如何检测角点呢?这个有好多种方法,比如以前提到的orb特征里的fast关键点的检测方式,就是一种角点检测方法。本文提到的harris也是一种角点检测方法,而且应该是名气很大的一种方法。除此之外,还有一些其他的角点检测方法,比如Shi-Tomasi算法、SUSAN算子等。
2. harris角点检测
2.1 原理
由1.1中所述,我们知道在一个角点处设置一个滑动窗口,这个窗口无论朝哪个方向滑动,对应位置上的亮度都会有很大变化。对应如下公式
\[E(u,v) = \sum _{x,y} w(x,y)[ I(x+u,y+v) - I(x,y)]^{2}\]
其中: - w(x,y)是滑动窗口系数,系数越大,代表这个位置上的亮度差异对结果所占权重更大。一般使用二维高斯窗口 - (u,v)是一个确定位移 - I(x,y)是在位置(x,y)的亮度值,(x,y)是在滑动窗口范围内的一个点
上述公式中,有如下一项存在操作空间
\[[I(x+u,y+v) - I(x,y)]^{2}\]
可以泰勒展开近似成
\[ [ I(x,y) + u I_{x} + vI_{y} - I(x,y)]^{2} \]
消去并展开方程,带入原式得
\[ E(u,v) \approx \sum_{x,y} w(x,y)(u^{2}I_{x}^{2} + 2uvI_{x}I_{y} + v^{2}I_{y}^{2}) \]
写成矩阵形式是(可以这样写是因为\((u,v)\)仅仅代表一个移动方向,与窗口的大小、系数都不相关):
\[ E(u,v) \approx \begin{bmatrix} u & v \end{bmatrix} \left ( \displaystyle \sum_{x,y} w(x,y) \begin{bmatrix} I_x^{2} & I_{x}I_{y} \\ I_xI_{y} & I_{y}^{2} \end{bmatrix} \right ) \begin{bmatrix} u \\ v \end{bmatrix} \]
可以定义矩阵M为
\[ M = \displaystyle \sum_{x,y} w(x,y) \begin{bmatrix} I_x^{2} & I_{x}I_{y} \\ I_xI_{y} & I_{y}^{2} \end{bmatrix} \]
现在式子变成
\[ E(u,v) \approx \begin{bmatrix} u & v \end{bmatrix} M \begin{bmatrix} u \\ v \end{bmatrix} \]
我们知道,如果是角点的话,无论\((u,v)\)往哪个方向,\(E(u,v)\)的值都会变化很大,而这个性质是由二维矩阵\(M\)决定的。或者说,这个性质是由矩阵M的特征值与特征向量决定的。在特征值大的特征向量方向,\(E(u,v)\)的值变化较快,在特征值较小的特征向量方向,\(E(u,v)\)的值变化较慢
上式如果左值固定,这个式子本质上是一个椭圆,椭圆的扁率与尺寸是由M的特征值\(\lambda_1、\lambda_2\)决定的,椭圆的方向是由M的特征矢量决定的。假设椭圆方程如下
\[ \begin{bmatrix} u & v \end{bmatrix} M \begin{bmatrix} u \\ v \end{bmatrix} = 1 \]
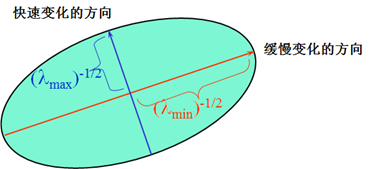
因此由矩阵M的特征值\(\lambda_1、\lambda_2\)的情况,可以将图像上的一个点分为三种情况: 1. 图像中边缘上的点。一个特征值大,另一个特征值小,即\(\lambda_1\gg \lambda_2\)或\(\lambda_2\gg \lambda_1\),在窗口朝某一方向滑动时,E的值变化明显,其他方向上不明显。 2. 图像中平面上的点。两个特征值都小,且近似相等。窗口朝各个方向上滑动,E的值变化都不明显。 3. 图像中角点。两个特征值都大,且近似相等。窗口朝每个方向滑动,E的值都会有很明显的变化。
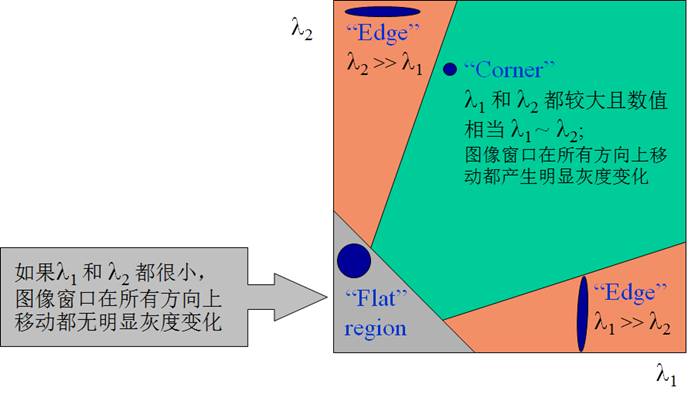
上述分析过后,我们知道如何使用M矩阵的特征值来判断一个点是边缘点、平面点还是角点。Harris提出可以计算一个harris角点响应值R来判断一个点是否是角点,而无需计算具体的矩阵特征值。R的计算公式如下:
\[ R=det \boldsymbol{M} - \alpha(trace\boldsymbol{M})^2 \]
其中: - \(det\boldsymbol{M}\)是矩阵M的行列式,并且\(det\boldsymbol{M} = \lambda_1\lambda_2 = AC-B^2\),A,B,C,D是M矩阵的四个元素 - \(trace\boldsymbol{M}\)是矩阵M的直迹,并且\(trace\boldsymbol{M}=\lambda_2+\lambda_2 = A+C\) - \(\alpha\)是一个经验系数,通常取值范围在0.04~0.06。下文还会对这个系数进行探讨。
至于为什么Harris响应值R如此定义,可以由下图知道原因。
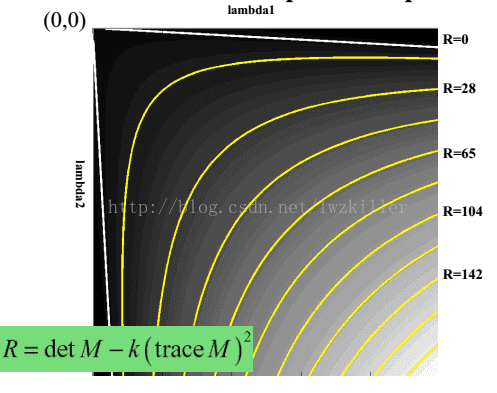
2.2 实际代码实现步骤
在上述原理讲解完毕后,代码实现主要可以分为五步: 1. 分别计算像素I(x,y)在x,y方向的梯度,使用sobel算子: \[I_x=\frac{\partial I}{\partial x}=I\otimes(-1\ 0\ 1),I_y =\frac{\partial I}{\partial x}=I\otimes(-1\ 0\ 1)^T\]
计算两个方向梯度的乘积: \[ I_x^2=I_x\cdot I_y,I_y^2=I_y\cdot I_y,I_{xy}=I_x\cdot I_y \]
生成高斯系数窗口,并最终确定M矩阵(前三步都是为了确定矩阵M)。
依据M矩阵计算每个像素的harris响应值R,并设置一个阈值,小于阈值的清零。
在\(3\times3或5\times5\)的领域内进行非极大值抑制,局部最大值点即为图像中的角点。
非极大值抑制原理是,在一个窗口内,如果有多个角点则用值最大的那个角点,其他的角点都删除。这样做可以祛除一些黏在一起的角点,好处是可以防止角点太密集,出现一小撮全是角点的情况。
2.3 harris角点性质
2.3.1 旋转不变性
由我们上述讲解的原理可知,当旋转发生时,矩阵M确定的椭圆也会发生旋转,但是椭圆的长短轴的大小是不会变化的。而椭圆的长短轴是矩阵M的特征值平方根的倒数,也就是说矩阵的特征值不会发生变化,所以harris响应值的大小也不会发生变化。因此harris角点检测具有旋转不变性。
2.3.2 光照不敏感
这是因为我们在进行harris响应值的计算时,并没有直接使用像素亮度信息,而是使用了像素亮度的梯度信息。但由于梯度信息对于像素亮度的拉升与收缩变化并不敏感,就算光照条件发生变化导致像素亮度整体发生变化,也不会影响harris响应值的极值点出现的位置。最多由于阈值的选择,会影响检测到的角点数量而已。
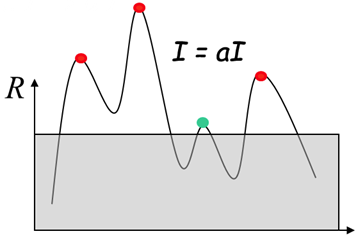
2.3.3 不具备尺度不变
这一点同样容易理解,下图解释的尤其形象。
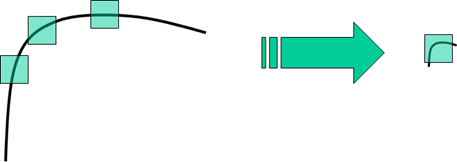
2.3.4 参数\(\alpha\)的意义
假设已经得到了矩阵M的特征值\(\lambda_1\ge\lambda_2\ge0\),令\(\lambda_2=k\lambda_1,0\le k\le 1\)。由特征值与矩阵M的直迹和行列式的关系可得:
\[ det\boldsymbol{M}=\prod_i\lambda_i \ \ \ \ \ \ trace\boldsymbol{M}=\sum_i\lambda_i \]
所以角点的响应值为
\[ R=\lambda_2\lambda_2=\alpha(\lambda_2+\lambda_2)^2=\lambda^2(k-\alpha(1+k)^2) \]
若有R不小于0,则
\[ 0\le \alpha \le\frac{k}{(1+k)^2}\le0.25 \]
并且有如下结论:增大α的值,将减小角点响应值R,降低角点检测的灵性,减少被检测角点的数量;减小α值,将增大角点响应值R,增加角点检测的灵敏性,增加被检测角点的数量。
2.4 harris角点检测的opencv接口与自己的c++实现
见我的github
3. 总结
由上面的描述我们知道了什么是角点,harris角点响应值的定义等,其实角点的定义都是相同的,只是不同的角点检测方法定义了不同的角点响应值的计算方式罢了。上述推导了最出名的harris响应值的定义公式,还有其他的角点响应值,比如Shi-Tomasi角点响应值是矩阵M较小的那个特征值。这种方法不仅充分,而且在很多情况下(比如跟踪)会比harris更加有效。 # 4. 参考资料 - [1] https://docs.opencv.org/3.4.1/d4/d7d/tutorial_harris_detector.html - [2] https://www.cnblogs.com/ronny/p/4009425.html#4056636 - [3] https://blog.csdn.net/lwzkiller/article/details/54633670